Kezdőlap


Feladat:	F.2804	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Balogh József , Borsányi Ákos , Erben Péter , Imreh Csanád
Füzet:	1990/december, 451 - 452. oldal		PDF \| MathML
Témakör(ök):	Derékszögű háromszögek geometriája, Egyenlő szárú háromszögek geometriája, Hozzáírt körök, Feuerbach-kör, Kúpszeletek érintői, Feladat
Hivatkozás(ok):	Feladatok: 1990/május: F.2804

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Az ábráról leolvasható, hogy az oldalfelező pontok és a háromszög $C$ csúcsa négyzetet határoznak meg.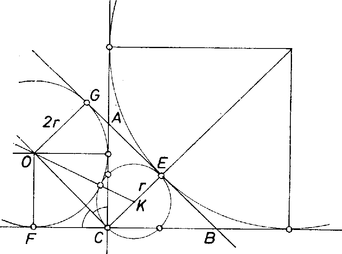

Az oldalfelező pontokon átmenő,

K

középpontú kör tehát

C

-n is átmegy, és sugara

(r)

feleakkora, mint a

C E

magasság. Az egyik befogóhoz írt kör

O

középpontja rajta van a

C

-ből húzott külső szögfelezőn, ami párhuzamos az átfogóval, ezért e hozzáírt kör

O G

sugara akkora, mint

C E

, azaz

2 r

.
Az

O F C

derékszögű háromszög befogói

2 r

hosszúságúak, így átfogója

O C = 2 r \sqrt[]{2}

.
Az

O C K

derékszögű háromszög befogói

2 r \sqrt[]{2}

és

r

, ezért átfogója

O K = = \sqrt[]{8 r^{2} + r^{2}} = 3 r

. A két kör középpontjának távolsága tehát a sugarak összege, ami azt jelenti, hogy a két kör érinti egymást. (Az átfogóhoz írt kör nyilván

E

-ben érinti

A B

-t, akárcsak az oldalfelező pontokon átmenő kör.)

Erben Péter (Bp. Berzsenyi Dániel Gimn., III. o. t.)

II. megoldás. A feladat állítása speciális esete a Feuerbach-tételnek, amely szerint a háromszög Feuerbach-köre érinti a háromszög oldalegyeneseit érintő köröket; a beírt kört magába foglalja, a hozzáírt köröket pedig kívülről érinti. A tétel bizonyítása megtalálható pl. Reiman István: A geometria és határterületei c. könyvének 71. oldalán. Megjegyezzük, hogy az idézett könyvben a beírt körre vonatkozó állítás igazolása található meg. Szorgalmas megoldóink nemcsak hivatkoztak a könyvre, hanem be is bizonyították a hozzáírt körre vonatkozó állítást.