Kezdőlap


Feladat:	F.2754	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Balogh 171 J. , Harcos G. , Kiss 128 I. , Kőrösi A. , Kovács Ágnes , Nagy G. P. , Nagypál Éva , Podoski Károly. , Szekeres B. , Szendrői B. , Tokodi T. , Vidács Attila , Virág B. , Zircher P.
Füzet:	1990/március, 108 - 109. oldal		PDF \| MathML
Témakör(ök):	Irracionális egyenlőtlenségek, Geometriai egyenlőtlenségek, Koszinusztétel alkalmazása, Vektorok vektoriális szorzata, Feladat
Hivatkozás(ok):	Feladatok: 1989/szeptember: F.2754

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Ha $a$ , $b$ , $c$ valós számok, akkor mindhárom gyökjel alatt nemnegatív szám áll, mert az első kifejezés ${(a - b)}^{2}$ és ${(a + b)}^{2}$ , a második ${(b - c)}^{2}$ és ${(b + c)}^{2}$ , a harmadik pedig ${(a - c)}^{2}$ és ${(a + c)}^{2}$ közé esik. Így a feladat állítása minden $a$ , $b$ , $c$ valós számhármasra értelmes. Az is világos, hogy mindkét oldal nemnegatív, így négyzetre emelhetünk, ez az egyenlőtlenség érvényén nem változtat. A négyzetreemelés és a rendezés elvégzése után a

\begin{matrix} 2 \sqrt[]{a^{2} b^{2} + a^{2} c^{2} + b^{4} + b^{2} c^{2} - a b^{3} - a b c^{2} - a^{2} b c - b^{3} c + b^{2} a c} \geq a b + a c + b c - 2 b^{2} \end{matrix}

egyenlőtlenséghez jutunk. A bal oldal mindig nemnegatív. Ha a jobb oldal negatív, akkor kész vagyunk: az egyenlőtlenség igaz. Ha pedig mindkét oldal nemnegatív, akkor négyzetre emelhetünk. Ezt elvégezve, és a kapott egyenlőtlenséget rendezve a valóban igaz

\begin{matrix} 3 {(a b + b c - a c)}^{2} \geq 0 \end{matrix}

egyenlőtlenséghez jutunk. Ezzel egyenlőtlenségünket minden esetre beláttuk. Egyenlőség pontosan akkor áll fenn, ha

a c = a b + b c

, és

a b + a c + b c - 2 b^{2} \geq 0

Kovács Ágnes (Jászberény, Lehel Vezér Gimn., IV. o. t.)

II. megoldás. Az egyenlőtlenséget geometriai úton bizonyítjuk. Azt fogjuk belátni, hogy ha

a

b

c

valós számok, akkor

\begin{matrix} \sqrt[]{| a |^{2} + | b |^{2} - | a | | b |} + \sqrt[]{| b |^{2} + | c |^{2} - | b | | c |} \geq \sqrt[]{| a |^{2} + | c |^{2} + | a | | c |} . \end{matrix}

(1)

Itt a bal oldal kisebb, a jobb oldal nagyobb a bizonyítandó egyenlőtlenség megfelelő oldalánál, tehát a fenti egyenlőtlenségből már következik a feladat állítása.
Az (1) belátásához tekintsünk a síkon négy pontot,

O

A

B

C

-t, úgy hogy

O A = | a |

O B = | b |

O C = | c |

, továbbá

A O B ∢ = B O C ∢ = 60^{\circ}

A O C ∢ = 120^{\circ}

legyen (1. ábra).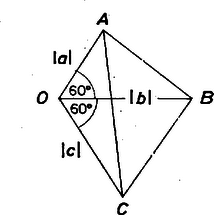

1. ábra

A koszinusz tétel szerint

\begin{matrix} \bar{A B} = \sqrt[]{O A^{2} + O B^{2} - 2 O A \cdot O B \cdot cos 60^{\circ}} = \sqrt[]{a^{2} + b^{2} - | a | | b |}, \end{matrix}

ugyanígy

\begin{matrix} \bar{B V} = \sqrt[]{b^{2} + c^{2} - | b | | c |} és \bar{A C} = \sqrt[]{O A^{2} + O C^{2} - 2 O A \cdot O C cos 120^{\circ}} = \\ = \sqrt[]{a^{2} + c^{2} + | a | | c |} . \end{matrix}

Az (1) egyenlőtlenség tehát éppen az

A B + B C \geq A C

háromszögegyenlőtlenség, s így nyilvánvalóan igaz.
Vidács Attila (Bp., Táncsics M. Gimn., III. o. t.)

Megjegyzés. Nyilvánvaló, hogy (1)-ben egyenlőség pontosan akkor áll, ha

A

B

C

egy egyenesbe esik (2. ábra).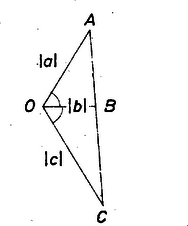

2. ábra

Ekkor az

O A C

háromszög kétszeres területe,

| a | | c | sin 120^{\circ}

egyenlő az

O A B

és

O B C

háromszögek kétszeres területének összegével,

| b | (| a | + | c |) sin 60^{\circ}

-kal. Innen

| b | (| a | + | c |) = | a | | c |

. Ezenkívül szükséges, hogy (1) megegyezzék a feladatbeli egyenlőtlenséggel, tehát

| a | | b | = a b

| a | | c | = a c

| b | | c | = b c

teljesüljön, azaz

a

b

és

c

előjele azonos legyen.