Kezdőlap


Feladat:	F.2744	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Balogh 171 J. , Benczúr P. , Boda Z. , Bokor P. , Csikász T. , Farkas Judit , Harcos G. , Hausel T. , Hídvégi Z. , Kovács 998 P. , Lois L. , Macskási Zs. , Mezei J. , Mohai Zsuzsa , Nagy 124 G. , Oláh G. , Papp 613 F. , Peták A. , Podoski Károly. , Stojan R. , Sustik M. , Szabó 972 S. , Szekeres B. , Szemerédi F. , Tokodi T. , Tóth 509 P. Z. , Tuba J. , Weisz Cs.
Füzet:	1989/december, 450 - 451. oldal		PDF \| MathML
Témakör(ök):	Szélsőérték differenciálszámítással, Másodfokú (és arra visszavezethető) egyenletek, Trigonometrikus egyenletek, Trigonometriai azonosságok, Egyenlő szárú háromszögek geometriája, Beírt kör, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1989/április: F.2744

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a háromszögbe írt kör középpontja $O$ , sugara $ϱ$ , és használjuk az ábra további jelöléseit is.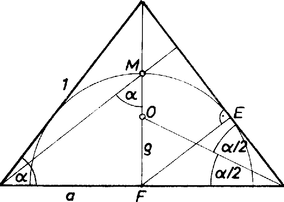

Az ábra alapján rögtön láthatjuk, hogy

\begin{matrix} a = cos α, \end{matrix}

továbbá

\begin{matrix} ϱ = cos α \cdot tg \frac{α}{2} . \end{matrix}

Vizsgáljuk

ϱ

értékét

α

függvényeként. Ez a függvény a

[0; \frac{π}{2}]

intervallumban folytonos, tehát ott van maximuma. Tekintve, hogy a függvény az intervallum végpontjaiban zérus, egyéb helyeken pedig pozitív, maximumát a

(0; \frac{π}{2})

nyílt intervallumban veszi fel. Világos, hogy

ϱ

deriválható függvénye

α

-nak, ezért a keresett maximum olyan helyen lehet, ahol

ϱ' = 0

. Deriválás előtt

ϱ

fenti kifejezését kissé átalakítjuk. Ehhez felhasználjuk a

cos α = 2 \cdot cos^{2} \frac{α}{2} - 1

és a

sin α = 2 \cdot sin \frac{α}{2} \cdot cos \frac{α}{2}

azonosságokat.

\begin{matrix} ϱ = tg \frac{α}{2} (2 \cdot cos^{2} \frac{α}{2} - 1) = 2 \cdot sin \frac{α}{2} \cdot cos \frac{α}{2} - tg \frac{α}{2} = sin α - tg \frac{α}{2} . \end{matrix}

A derivált:

\begin{matrix} ϱ' = cos α - \frac{1}{2 \cdot cos^{2} \frac{α}{2}} . \end{matrix}

Az előbb használt azonosságok közül az elsőt ismét alkalmazva:

\begin{matrix} ϱ' = cos α - \frac{1}{1 + cos α} . \end{matrix}

A szélsőérték helyét így a

\begin{matrix} cos α - \frac{1}{1 + cos α} = 0 \end{matrix}

egyenletből kaphatjuk meg, azaz:

\begin{matrix} cos^{2} α + cos α - 1 = 0, \end{matrix}

(1)

innen

\begin{matrix} cos α = \frac{- 1 \pm \sqrt[]{5}}{2} . \end{matrix}

Mivel

0 < α < \frac{π}{2}

cos α = \frac{\sqrt[]{5} - 1}{2}

, s így a háromszög alapja

2 a = \sqrt[]{5} - 1

. A

cos α

függvény a szóban forgó intervallumban kölcsönösen egyértelmű, ezért egyetlen olyan

α

létezik, amely mellett

ϱ

maximális. (Azt, hogy létezik ilyen

α

, korábban már megindokoltuk.)
Nézzük ezután az alapra rajzolt és a szárakat érintő félkört. Ennek sugara

F E

. A feladat második állítása azt jelenti, hogy a maximális

ϱ

mellett

F M = F E

. Tudjuk, hogy a maximális

ϱ

értékhez tartozó

α

-ra fennáll (1), azaz

\begin{matrix} \begin{matrix} cos^{2} α + cos α = 1, és így \\ cos^{2} α + cos α = sin^{2} α + cos^{2} α, amiből \\ cos α = sin^{2} α . \end{matrix} \end{matrix}

Ennek az egyenletnek mindkét oldalát

ctg α

-val szorozva :

\begin{matrix} cos α \cdot ctg α = sin α \cdot cos α . \end{matrix}

(2)

Az ábráról könnyen leolvasható, hogy

F M = cos α \cdot ctg α

és

F E = sin α \cdot cos α

, ezért (2) éppen azt jelenti, hogy

F M = F E