Kezdőlap


Feladat:	F.2732	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Balogh 171 József , Boldizsár T. , Harcos G. , Kovács 271 Ágnes , Macskási Zs. , Majtényi Márta , Nagy 124 G. , Siklér F. , Sustik M. , Tuba I.
Füzet:	1989/november, 381 - 382. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Algebrai átalakítások, Tengelyes tükrözés, Ceva-tétel, Súlyvonal, Szögfelező egyenes, Feladat
Hivatkozás(ok):	Feladatok: 1989/február: F.2732

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

a) Legyen az $a$ oldal felezőpontja $A_{1}$ , a $b$ oldal felezőpontja $B_{1}$ , az $A A_{1}$ súlyvonal $A D$ szögfelezőre vonatkozó tükörképének és az a oldalnak a metszéspontja pedig $A_{0}$ . A további jelöléseket az ábrán találjuk.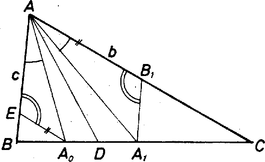

\frac{B A_{0}}{A_{0} C}

arányt akarjuk meghatározni. Az

A_{0}

ponton át

A C

-vel húzott párhuzamos a

c

oldalt az

E

pontban metszi. Az

A_{1} B_{1}

és az

A B

szakaszok párhuzamosak, ezért az ábrán két ívvel jelölt szögek egyenlőek. Az

A D

szögfelezőre vonatkozó szimmetria révén az egy ívvel jelölt szögek is egyenlők. Ezért az

A E A_{0}

és az

A B_{1} A_{1}

háromszögek hasonlóak,

\begin{matrix} \frac{A_{0} E}{E A} = \frac{A_{1} B_{1}}{B_{1} A} . \end{matrix}

Ezt így is írhatjuk:

\begin{matrix} \frac{A_{0} E}{c - E B} = \frac{A_{1} B_{1}}{B_{1} A} = \frac{\frac{c}{2}}{\frac{b}{2}} = \frac{c}{b} . \end{matrix}

(1)

Könnyen látható, hogy

E B A_{0}

és az eredeti

A B C

háromszög hasonló és ezért

\begin{matrix} \frac{A_{0} E}{B A_{0}} = \frac{b}{a} és \frac{E B}{B A_{0}} = \frac{c}{a} . \end{matrix}

Ebből a két egyenlőségből

A_{0} E

-t és

E B

-t kifejezve, majd (1)-be helyettesítve:

\begin{matrix} \frac{B A_{0} \cdot \frac{b}{a}}{c - B A_{0} \cdot \frac{c}{a}} = \frac{c}{b}, \end{matrix}

amelyből

\begin{matrix} \frac{B A_{0}}{a - B A_{0}} = \frac{c^{2}}{b^{2}}, \end{matrix}

vagyis

\begin{matrix} \frac{B A_{0}}{A_{0} C} = \frac{c^{2}}{b^{2}} . \end{matrix}

A feladat első kérdésére tehát azt felelhetjük, hogy egy tükörkép a szemközti oldalt a csúcsból kiinduló oldalak négyzetének arányában osztja.
b) A feladat második kérdésére igenlő a válasz. Világos ugyanis, hogy

A_{0}

és a hasonló szerepű

B_{0}

, illetve

C_{0}

a háromszög oldalainak belső pontjai, továbbá az a)részben látott eredmény alapján:

\begin{matrix} \frac{B A_{0}}{A_{0} C} \cdot \frac{C B_{0}}{B_{0} A} \cdot \frac{A C_{0}}{C_{0} B} = \frac{c^{2}}{b^{2}} \cdot \frac{a^{2}}{c^{2}} \cdot \frac{b^{2}}{a^{2}} = 1, \end{matrix}

ebből pedig a Ceva-tétel megfordítása szerint az következik, hogy a három egyenes egy ponton megy keresztül.