Kezdőlap


Feladat:	F.2719	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Benczúr P. , Benkő P. , Podoski Károly. , Tornyi Lajos
Füzet:	1989/május, 210 - 211. oldal		PDF \| MathML
Témakör(ök):	Összefüggések binomiális együtthatókra, Polinomok, Teljes indukció módszere, Feladat
Hivatkozás(ok):	Feladatok: 1988/december: F.2719

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük $P (x)$ elsőrendű különbség-polinomját, a $P (x + 1) - P (x)$ polinomot $P_{1} (x)$ -szel (ez nyilván $(n - 1)$ -edfokú), a másodrendű különbség-polinomja legyen $P_{2} (x) = P_{1} (x + 1) - P_{1} (x)$ (ennek a polinomnak $n - 2$ a foka), és általában hasonlóan definiáljuk a $k$ -adrendű különbség-polinomot: $P_{k} (x) = P_{k - 1} (x + 1) - P_{k - 1} (x)$ . A $k$ -ra vonatkozó indukcióval könnyen látható, hogy $P_{k} (x)$ foka $n - k$ , így a $P_{n} (x)$ polinom már konstans. Ezt a konstanst (és a különbség-polinomok közbülső értékeit) adatainkból ismételt kivonással határozhatjuk meg: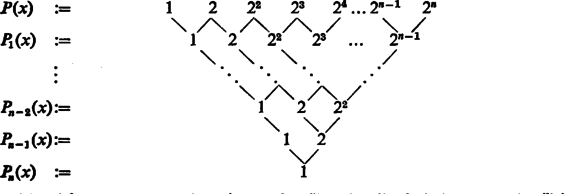

P_{n} (x)

tehát az azonosan

1

polinom. Ebből

P (n + 2)

értékét a következőképpen kaphatjuk meg:

\begin{matrix} P (n + 2) & = P (n + 1) + P_{1} (n + 1) = P (n + 1) + P_{1} (n) + P_{2} (n) \\ = P (n + 1) + P_{1} (n) + P_{2} (n - 1) + P_{3} (n - 1) = ... \\ = P (n + 1) + P_{1} (n) + P_{2} (n - 1) + P_{3} (n - 2) + ... + P_{n - 1} (2) + P_{n} (2) = \\ = 2^{n} + 2^{n - 1} + 2^{n - 2} + ... + 2^{2} + 2 + 1 = \\ = 2^{n + 1} - 1 \end{matrix}

(előbbi táblázatunkban ez az utolsó "átló'' összege).

II. megoldás. Felhasználjuk az ismert

\begin{matrix} \sum_{i = 0}^{k - 1} (\binom{k - 1}{i}) = 2^{k - 1} \end{matrix}

azonosságot. Értelmezzük a

q_{0} (x) = 1

, ill.

k ≧ 1

-re a

\begin{matrix} q_{k} (x) = (\binom{x - 1}{k}) = \frac{(x - 1) \cdot (x - 2) \cdot ... \cdot (x - k)}{k!} \end{matrix}

k

-adfokú polinomokat. Ekkor a

\begin{matrix} q (x) = q_{0} (x) + q_{1} (x) + ... + q_{k} (x) + ... + q_{n} (x) \end{matrix}

polinom az

x

= 1, 2,

...

n + 1

helyeken rendre a

2^{0}

2^{1}

2^{2}

...

2^{n}

értékeket veszi fel. Ha ugyanis

x = k

, akkor

\begin{matrix} q_{0} (k) + q_{1} (k) + ... + q_{k - 1} (k) = (\binom{k - 1}{0}) + (\binom{k - 1}{1}) + ... + (\binom{k - 1}{k - 1}) = 2^{k - 1}, \end{matrix}

és

t ≧ k

esetén

q_{1} (k) = 0

. Így az

n

-edfokú

q (x)

polinom az

x

= 1, 2,

...

n + 1

helyeken éppen azokat az értékeket veszi fel, mint

P (x)

. Ha azonban két

n

-edfokú polinom

(n + 1)

különböző helyen megegyezik, akkor azonos; tehát

q (x)

maga a keresett polinom. Ennek pedig az

x = n + 2

helyen felvett értéke:

\begin{matrix} \sum_{i = 0}^{n} (\binom{n + 1}{i}) = 2^{n + 1} - 1. \end{matrix}

Tornyi Lajos (Bp. Fazekas M. Gimn. IV. o. t.)