Kezdőlap


Feladat:	F.2713	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1989/október, 297 - 298. oldal		PDF \| MathML
Témakör(ök):	Páros gráfok, Ponthalmazok távolsága, Egyéb sokszögek geometriája, Szabályos sokszögek geometriája, Feladat
Hivatkozás(ok):	Feladatok: 1988/november: F.2713

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Ha a szabályos sokszög oldalainak száma páros, akkor az átmérője két szemközti csúcs távolsága. Vágjuk el ezt a sokszöget két részre egy oldalának felező merőlegesével. Ekkor mindkét rész átmérője a kiszemelt oldal felezőpontját a szemközti oldal egyik végpontjával összekötő szakasz hossza lesz, ami nyilván kisebb, mint a szabályos sokszög átmérője.
Legyen ezután a szabályos sokszög oldalainak száma $2 n + 1$ . Akárhogyan osztjuk két sokszögre ezt az alakzatot, (nem feltétlenül egy egyenessel vágva el), az egyik részben legalább $n + 1$ egymás utáni csúcs lesz. Ennek a résznek az átmérője megegyezik az eredeti sokszög átmérőjével. Tehát a feltételnek a páratlan oldalú sokszögek felelnek meg.

II. megoldás. Gráfok segítségével megmutatjuk, hogy egy páratlan oldalszámú szabályos sokszög csúcsait két osztályba sorolva, valamelyik osztályban biztosan található két olyan csúcs, amelyeknek a távolsága a sokszög átmérője. Jelölje

G

azt a gráfot, amelynek szögpontjai a sokszög csúcsai, és két szögpontját akkor köti össze él, ha azok távolsága egyenlő a sokszög átmérőjével. Így minden pont éppen két másikkal lesz összekötve. Legyen

A_{1}

az egyik csúcs, ebből induljon egy él

A_{2}

-be. Az

A_{2}

szögpont

A_{1}

-en kívül még egy csúccsal össze van kötve, jelölje azt

A_{3}

. Az

A_{3}

-ból

A_{2}

-n kívül még megy él

A_{4}

-be,

A_{4}

-ből

A_{5}

-be, és így tovább. Ebben az

A_{1}, A_{2}, A_{3}, ...

sorozatban előbb-utóbb el kell jutnunk egy olyan

A_{k}

-hoz, amelyre az

A_{1}, A_{2}, ..., A_{k}

pontok még mind különbözők, de

A_{k + 1}

már megegyezik ezek valamelyikével,

A_{r}

-rel. Ebben az esetben

A_{r}

csak

A_{1}

lehet, hiszen másképpen

A_{r}

legalább 3 ponttal

(A_{r - 1}, A_{r + 1}, A_{k})

lenne összekötve.

A_{1} A_{2} ... A_{k}

tehát egy kör, így benne minden pontból két él fut ki.

1. ábra

Az itt fel nem sorolt csúcsokra folytatva az eljárást, végül

G

minden pontja belekerül egy-egy körbe. Két különböző körnek nem lehet közös pontja, mert abból legalább 3 él indulna ki. A

G

gráfnak tehát annyi pontja van, amennyi e körök hosszának az összege. Így lennie kell páratlan hosszú körnek is, ezért

G

nem páros gráf.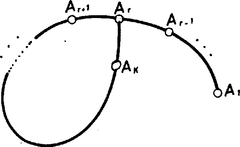

2. ábra