Kezdőlap


Feladat:	F.2594	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1987/február, 68 - 69. oldal		PDF \| MathML
Témakör(ök):	Eltolás, Terület, felszín, Paralelogrammák, Helyvektorok, Vektorok vektoriális szorzata, Feladat
Hivatkozás(ok):	Feladatok: 1986/szeptember: F.2594

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Húzzunk párhuzamosokat az $A B C D$ négyszög csúcsain át a négyszög átlóival (1/a, b ábrák). Az így kapott $P$ paralelogramma területe nyilván az $A B C D$ négyszög területének kétszerese, másfelől a $P$ oldalai a négyszög átlóival egyenlők, $P$ oldalainak szöge pedig a négyszög átlóinak szögével. Mivel a megadott $u$ , illetve $v$ vektorokkal történő eltolások során az átlók állása nem változik, az $A' B' C' D'$ négyszöghöz hasonlóan elkészített paralelogramma a $P$ -vel egybevágó, és így a két négyszög területe valóban egyenlő.

1.a ábra

1.b ábra

Megjegyzés. A fenti paralelogramma területe

e \cdot f \cdot sin (e, f)

, ahol

e

és

f

a négyszög átlói, azaz tetszőleges ‐ nem hurkolt ‐ négyszög területének kétszerese az átlók és az átlók szöge szinuszának a szorzata. Ez az összefüggés háromszögre is érvényes és ilyenkor a jól ismert

t = \frac{1}{2} a \cdot b \cdot sin γ

alakot ölti. (Az átlók a háromszög oldalaiba mennek át.)

Az alábbi változat teljes egészében a vektorok nyelvén írja le a fenti megoldást. Az ábrán

b - c

javítandó

b - a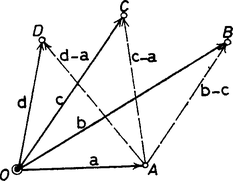

-ra.

2. ábra

II. megoldás. Fejezzük ki az

A B C D

négyszög csúcsaihoz húzott a, b, c d helyvektorokkal az

A B

A D

és az

A C

vektorokat a 2. ábra szerint. Ezeknek a vektoroknak a vektoriális szorzatával a négyszög kétszeres területe kifejezhető :

\begin{matrix} 2 t = (b - a) \times (c - a) + (c - a) \times (d - a), \end{matrix}

ahol t olyan vektor, amelynek hossza

t

, merőleges a négyszög síkjára és a pozitív féltérbe mutat.
A vektoriális szorzat tulajdonságai alapján

\begin{matrix} 2 t = (b - a) \times (c - a) - (d - a) \times (c - a) = & (1) \\ = (b - a - d + a) \times (c - a) = (b - d) \times (c - a) . \end{matrix}

Az (1) alapján az

A' B' C' D'

négyszög kétszeres területvektora

\begin{matrix} 2 t' = ((b + v) - (d + v)) \times ((c + u) - (a + u)) = & (2) \\ = (b - d) \times (c - a) . \end{matrix}

(1)-ből és (2)-ből pedig következik a feladat állítása.