Kezdőlap


Feladat:	F.2565	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Benczúr A. , Bereczky Á. , Csott R. , Cynolter G. , Dinnyés Enikő , Grallert Ágnes , Gyuris V. , Hajdú G. , Heller Judit , Horváth E. , Majoros L. , Majzik I. , Pál G. , Tasnádi T. , Tóth 324 T.
Füzet:	1986/november, 365 - 367. oldal		PDF \| MathML
Témakör(ök):	Háromszögek egybevágósága, Poliéderek átdarabolása, Vetítések, Derékszögű háromszögek geometriája, Középvonal, Térgeometriai bizonyítások, Tetraéderek, Feladat
Hivatkozás(ok):	Feladatok: 1986/január: F.2565

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Látni fogjuk, hogy a feladat b) és c) állítása csak az $f > e (> 0)$ nagyságviszony mellett érvényes.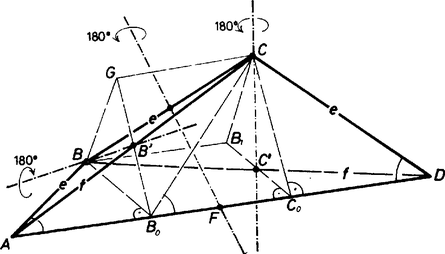

1. ábra

Legyen

B

és

C

vetülete

A D

-re

B_{0}

, ill.

C_{0}

, a

C

csúcs vetülete az

A B D

síkra

C'

, és

B

vetülete a

C_{0} C'

egyenesre

B_{1}

(1. ábra). Az

A D B

és

D A C

lapháromszögek egybevágók, mert ezen körüljárásaik szerinti első oldalpárjuk közös, a további kettő pedig a feltevés szerint egyenlő. Emiatt

B B_{0}

C C_{0}

magasságaik is egyenlők.
Az adott

C C_{0} C' ∢ = 60^{\circ}

alapján a

C C_{0} C'

derékszögű háromszögből

\begin{matrix} C' C_{0} = \frac{C C_{0}}{2} = \frac{B B_{0}}{2} = \frac{B_{1} C_{0}}{2}, \end{matrix}

hiszen

C' C_{0}

merőleges

A D

-re és

B B_{1}

-re, tehát

B B_{1} ∥ A D

. Eszerint

C'

felezi a

B_{1} C_{0}

szakaszt, továbbá a

C C_{0} B_{1}

háromszög egyenlő oldalú.
Másrészt

C

benne van a

B_{1} C_{0}

szakasz felező merőleges síkjában, ez pedig azonos a

B B_{0}

szakasz felező merőleges síkjával, tehát az adatok szerint

\begin{matrix} B_{0} C = B C = e = D C . \end{matrix}

(1)

1. Ha mármost

e = A B < D B = f

, akkor a közös befogójú

B B_{0} A

és

B B_{0} D

háromszögekből

B_{0} A < B_{0} D

, tehát

B_{0} D C

valódi háromszög és egyenlő szárú. Ebben a

B_{0} D

alapon fekvő szögek hegyesszögek, egyszersmind

B A D ∢

is hegyesszög. Így

C_{0}

B_{0}

A D

élszakaszon vannak és harmadolják azt. Jelöljük

A D

hosszát

3 g

-vel, ekkor az

A D C

háromszögből

\begin{matrix} g = D C_{0} = D C \cdot cos C D A ∢ = \frac{A D^{2} - A C^{2} + C D^{2}}{2 \cdot D A} = \frac{9 g^{2} - (f^{2} - e^{2})}{6 g}, \end{matrix}

és

A D

keresett kifejezése:

\begin{matrix} A D^{2} = 9 g^{2} = 3 (f^{2} - e^{2}), \end{matrix}

ami a most vizsgált esetben pozitív. Hozzátesszük, hogy mivel az

A D^{2} = (f + e) (3 f - 3 e)

felbontás első tényezője az

A D B

háromszög révén nagyobb, mint

A D

, azért a második tényezőre

A D < 3 f - 3 e

, és az

f + e > 3 f - 3 e

egyenlőtlenségből

2 e > f

feltétele annak, hogy a háromszög létrejöhessen. Ugyanez az egybevágó

B C A

és

B C D

lapokból is kiadódik.
2. Ha viszont

e = A B > D B = f

, akkor

A B_{0} > D B_{0} = A C_{0}

. Így

B_{0}

C_{0} D

félegyenesen van, másrészt (1) szerint

C

-től ugyanannyira, mint

D

, tehát

B_{0}

azonos

D

-vel. Ezért az

A D B ∢ = D A C ∢

derékszög, tehát ekkor

A D^{2} = A B^{2} - B D^{2} = e^{2} - f^{2}

(2. ábra). Ide kapcsoljuk mindjárt, hogy

e = f

nem lehetséges. Akkor ugyanis

C_{0}

egybeesnék

B_{0}

-lal, és

B_{1}

B

-vel, így ‐ hacsak

A D > 0

‐,

B B_{0} = C B_{0} < B A = e = B C

lenne, és a

B B_{0} C ∢

nem lehetne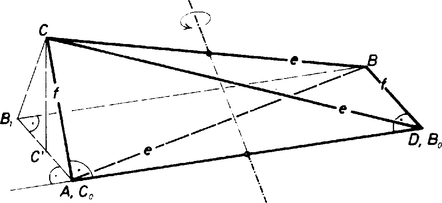

60^{\circ}

-os.

2. ábra

Láttuk, hogy az 1. nagyságviszony mellett

C_{0}

felezi a

B_{0} D

szakaszt, és

C_{0} C' ∥ B_{0} B

, így

C_{0} C' = B_{0} B / 2

éppen középvonala a

B B_{0} D

háromszögnek, tehát

C'

rajta van a

B D

élen (felezi azt). Így a

B C D

lap tartalmazza az

A B D

-re merőleges

C C'

egyenest, tehát maga is merőleges az

A B D

lapsíkra, ahogy a feladat állítja.
Ugyanez a tény az

A C = f

élben metsződő lappárra abból adódik, hogy a testnek van olyan forgástengelye, amely körüli

180^{\circ}

-os elfordítással önmagába megy át. Ez a tengely az

A D

szakasz

F

felezőpontján megy át, merőleges az élre és benne van a

B (A D) C

lapszöget felező síkban. Könnyen adódik az előzőkből, hogy a tengely a

B C

élt is felezi. Így az

A

és

D

, valamint a

B

és

C

csúcspárok egymás helyére fordulnak, és a

B D

élnél levő derékszögű lapszög az

A C

élnél levő lapszögbe megy át, az is derékszög.
(Az

e > f

nagyságviszony esetében

C'

nincs rajta a

B D

szakaszon, előbbi érvelésünk alapja kiesik, nincs derékszög az

f

-élekben összefutó lappárok között. A forgástengely azonban ekkor is megvan.)
Rátérünk a c) állításra, de már csak az

e < f

esetben. Az első alkalmas metsző sík a

C C_{0} C'

, merőleges az

A D

élre. A

D C C_{0} C'

tetraédert a

C C'

tengely körül

180^{\circ}

-kal elfordítva

D

B

-be jut és

C_{0}

B_{1}

pontba, a

C C_{0} C'

síkmetszet helyben maradó és elforduló példányai együtt a

C C_{0} B_{1}

szabályos háromszöget alkotják. A második síkmetszet pedig az a

B B_{0} B'

, amelybe az első metszet az említett szimmetriával átmegy, tehát szintén merőleges

A D

-re,

B'

A C

él felezőpontja. Létrejön a

B B_{0} G

szabályos háromszög, egybevágó a

C C_{0} B_{1}

-gyel, és avval párhuzamos síkban fekszik, ezek az állítás szerinti hasáb alaplapjai; az oldalélek pedig

B_{0} C_{0}

B B_{1}

és

G C

Megjegyzések. 1. A vizsgált típusú tetraéderek (

e < f

esetén) könnyű példát nyújtanak testátdarabolásra. Bolyai Farkas tétele szerint bármely két egyenlő területű, egyenes vonalú síkidom véges sok lépésben átdarabolható egymásba, ezzel szemben a térben általában nem lehetséges ez két egyező térfogatú, síklapokkal határolt test között, csak bizonyos szoros feltételek mellett.
2. A térszemlélet gyakorlásául hozzáfűzzük: az

A D B

és

D A C

lapok a testtel együtt átmennek egymásba, tehát egyező körüljárásúan egybevágók, ha a testre mindkétszer kívülről nézünk rá. Az 1. ábrán viszont

A D B

és

D A C

ellentétes körüljárásúak. Ez abból adódik, hogy ott a

D A C

lapra kívülről nézünk rá, míg az

A B D

lapra a test belseje felől.