Kezdőlap


Feladat:	F.2563	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1986/október, 299 - 300. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Derékszögű háromszögek geometriája, Parabola, mint mértani hely, Feladat
Hivatkozás(ok):	Feladatok: 1986/január: F.2563

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen a rögzített $K$ kör sugara $R$ , középpontja $O$ , ennek és $F$ -nek közös vetülete $e$ -re $M$ , az $M F$ szakasz hossza pedig legyen $f$ . Jelölje egy tetszőleges vizsgálandó $k$ kör sugarát $r$ , középpontját $O_{1}$ , ennek vetületét az $M F$ egyenesre $O_{f}$ , végül a $k$ kör $F$ -ből húzott egyik érintőjének érintési pontját $E$ (1. ábr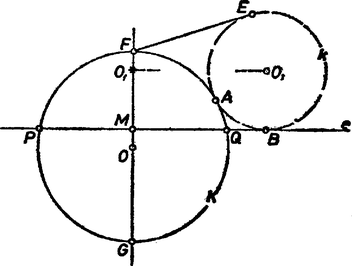a).

1. ábra

Pitagorasz tételét többször alkalmazva

\begin{matrix} F E^{2} = F O_{1}^{2} - O_{1} E^{2} = (F O_{f}^{2} + O_{f} O_{1}^{2}) - r^{2} = F O_{f}^{2} + (O O_{1}^{2} - O O_{f}^{2}) - r^{2} . \end{matrix}

(1)

Tekintsük az

M F

egyenesen az

M, O, F

és

O_{f}

pontok lehetséges elhelyezkedését (2/a, b ábrák)!

2.a ábra

2.b ábra

Mivel

F

és

O_{1}

e

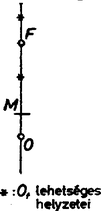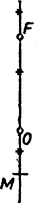egyenesnek ugyanazon az oldalán vannak, ezért

O_{f}

és

F

M

-ből nézve egy irányba esnek az

M F

egyenesen. Ezért

F O_{f} = | M F - M O_{f} | = | f - r |

, azaz (1) jobb oldalán az első tag,

F O_{f}^{2} = {(f - r)}^{2}

.
A két kör külső érintkezése miatt (1) jobb oldalán a második tag,

O O_{1}^{2} = {(R + r)}^{2}

.
A 2./a, b ábrákról az is leolvasható, hogy az

M F

irányt véve pozitívnak, az

M, O, F, O_{f}

pontok minden szóba jövő sorrendje mellett

\begin{matrix} O O_{f} = O F - F M + M O_{f} = R - f + r, \end{matrix}

tehát (1) jobb oldalán a harmadik tag,

O O_{f}^{2} = {(R - f + r)}^{2}

.
Azt kaptuk, hogy

\begin{matrix} F E^{2} = {(f - r)}^{2} + {(R + r)}^{2} - {(R - f + r)}^{2} - r^{2}, \end{matrix}

ahonnan a műveletek elvégzése után

\begin{matrix} F E^{2} = 2 R f \end{matrix}

adódik, és ez valóban csak a

K

körtől és az

e

helyzetétől függ.

II. megoldás. Az 1. ábra jelöléseit használva bebizonyítjuk, hogy a

k

körnek

K

-val és

e

-vel való

A

, ill.

B

érintkezési pontjait összekötő egyenes átmegy az

F

ponton.
Az

A O_{1} B

és

A O F

háromszögek hasonlók, mert egyenlő szárúak, illetve

O

-nál levő szárszögeik egyenlők. Ezek szerint az

O A F

és

O_{1} A B

szögek egyenlők és csúcsszögek,

A F

és

A B

pedig ellentétes irányúak. Ez egyértelmű állításunkkal.
Legyen most

K

-nak

F

-fel átellenes pontja

G

. Az

F G A

és

F B M

derékszögű háromszögek

F

-nél levő szöge közös, ezért hasonlók

F G : F A = F B : F M

, amiből

F A \cdot F B = F M \cdot F G

. Itt a jobb oldal állandó, a bal oldal pedig

F

-nek a

k

körre vonatkozó hatványa, ami egyenlő az

F

-ből húzott érintő négyzetével. Ezzel bebizonyítottuk az állítást.

Megjegyzések. 1. Könnyen belátható, hogy az

O_{1}

középpontok mértani helye egy parabola két szimmetrikus ívéből áll. A parabola fókusza

O

, vezéregyenese párhuzamos

e

-vel, tőle

R

távolságban halad,

e

-nek

F

-fel átellenes oldalán.
2. A II. megoldásban a derékszögű háromszög alapján

F M \cdot F G = F Q^{2} = F P^{2}

. Eszerint az

F

-ből húzott érintők érintési pontjai az

F

körüli

F Q

sugarú körön vannak,

e

-nek

F

-et tartalmazó partján. A pontos elemzést az olvasóra hagyjuk.