Feladat: F.2562 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Bereczky Á. ,  Cynolter G. ,  Dinnyés Enikő ,  Domokos M. ,  Drasny G. ,  Gyuris V. ,  Hajdú G. ,  Janszky J. ,  Keleti T. ,  Majoros L. ,  Pál G. ,  Ribényi Á. ,  Szalay Gy. ,  Szerdahelyi Judit ,  Tasnádi T. ,  Zaránd G. 
Füzet: 1987/január, 18 - 21. oldal  PDF  |  MathML 
Témakör(ök): Kombinatorika, Számelmélet alaptétele, Szélsőérték-feladatok differenciálszámítás nélkül, Feladat
Hivatkozás(ok):Feladatok: 1986/január: F.2562

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ha n vagy k értéke 1, akkor valamelyik számhalmazban egyetlen szám van. Ha ez a nulla, akkor valamennyi szorzat is nulla és így ekkor m=1.
A továbbiakban föltehető, hogy n és k nagyobbak egynél. Tetszőleges k- elemű Ak és n- elemű Bn halmazok elemeit külön-külön növekvő sorba rendezve a lehetséges n⋅k darab szorzatot írjuk be az 1. ábrán vázolt táblázat mezőibe.

 
 
1. ábra
 

A táblázat i-edik sorában (1≦i≦k) az Ak i-edik elemének és a Bn elemeinek a szorzata, a j-edik oszlopában (1≦j≦n) pedig a Bn j-edik elemének és az Ak elemeinek a szorzata áll.
Legfeljebb egy sor, illetve oszlop kivételével különböző számok állnak az egyes sorokban, illetve oszlopokban; ha Ak illetve Bn tartalmazza a nullát, akkor természetesen a megfelelő sor, illetve oszlop minden mezőjében nulla áll. Föltehető ugyanakkor, hogy Ak-ban és Bn-ben is szerepel a nulla, hisz egyébként egy-egy nem 0 elemet 0-val helyettesítve a különböző szorzatok száma nem nő.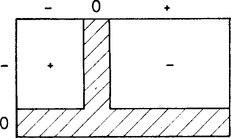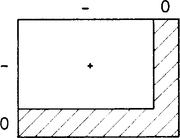
 
 
2.a ábra
 

 
 
2.b ábra
 

A táblázatban a szorzatok előjelét is feltüntettük. Előfordulhat, hogy az egyik halmaz vagy akár mindkettő azonos előjelű számokból áll; a táblázat szerkezete ilyenkor ennek megfelelően módosul (2/a, b ábrák). Előbbi feltevésünk szerint viszont más eset lényegében már nincsen, ugyanis a 2. ábrák további változatai az Ak, illetve a Bn elemeinek (-1)-gyel való szorzásával kaphatók, és ilyenkor a különböző szorzatok száma nem változik. A 2/a ábrán az Ak halmaz nem tartalmaz egyidejűleg pozitív és negatív elemeket is, ugyanez természetesen a Bn halmazra is fennállhat, de a két lehetőség szimmetrikus volta miatt ez nem ad új eredményt.
A nullaszorzatok elhagyásával táblázatunk minden esetben négy (1. ábra), kettő vagy pedig egy (2/a, b ábrák) résztáblázatra bomlik úgy, hogy az egyes résztáblázatokban minden szorzat első, illetve második tényezője ugyanolyan előjelű. Vegyük észre, hogy egy u×v méretű ilyen résztáblázat mindenképpen tartalmaz u+v-1 darab különböző számot, ennél többet azonban nem feltétlenül. Elegendő ezt abban az esetben igazolnunk, amikor a szorzatokat előállító tényezők mindegyike pozitív, a további esetekben a negatív tényezőket (-1)-gyel szorozva ilyen táblázathoz jutunk, és eközben nyilván nem változik a különböző szorzatok száma.
 
 
3. ábra
 

A tényezők növekvő elrendezése miatt a 3. ábra szaggatott útvonala mentén minden szorzat nagyobb, mint a megelőző, és így valóban u+v-1 különböző számot kapunk. (Ez egyébként bármely olyan u+v-1 hosszúságú útvonal mentén igaz, amelyik a bal felső sarokból vezet a jobb alsó sarokba). Ha pedig a kitöltést meghatározó tényezőket a 2 első u, illetve v darab hatványaként választjuk, akkor a szorzatok a 22 és a 2u+v közé eső 2-hatványok, és így a táblázatban éppen u+v-1 darab különböző szorzat szerepel.
Vegyük most szemügyre ennek alapján az 1, 2/a és 2/b ábrák lehetőségeit. Korábbi megjegyzéseink szerint elegendő ezeknek az eseteknek a vizsgálata.
A 2/b ábra egyetlen ,,résztáblájában'' a fentiek szerint legalább 1+(n-1)+(k-1)-1=n+k-2 a különböző szorzatok száma ‐ a 0-val együtt ‐ és mivel ez a leírt módon meg is valósítható, m≦n+k-2.
A 2/a ábrán a két résztáblázat ellenkező előjelű szorzatokat tartalmaz, így a részekből egy-egy különböző elemű maximális szorzathalmazt egyesítve továbbra sem kaphatunk egyenlő számokat. Az előbbiek szerint tehát a táblázatban ekkor a 0-val együtt legalább 1+2(k-1)+(n-1)-2=n+2k-4 (vagy a szimmetrikus esetben k+2n-4) különböző szorzat szerepel. Miután pedig k≧2 (és n≧2), az ilyen esetekben is van legalább n+k-2 különböző a létrejövő szorzatok között.
Meg kell még vizsgálnunk, hogy az 1. ábra legáltalánosabb esetében is találhatunk-e mindig n+k-2 különböző szorzatot. Az ellenkező előjelű résztáblák különböző elemekből álló maximális szorzathalmazai most is egyesíthetők, a kérdés az, hogy a négyféle lehetőség legalább mekkora elemszámot biztosít.
Legyen az Ak halmazban k1 és k2, a Bn-ben pedig n1 és n2 a negatív, illetve a pozitív elemek száma. (k1+k2=k-1 és n1+n2=n-1, és most k1, k2, n1, n2 pozitív mennyiségek.)
A korábbiak szerint az egyes negyedek ilyenkor egyenként legalább P1=k1+n1-1, N1=k1+n2-1, P2=k2+n2-1, illetve N2=k2+n1-1 darab különböző számot tartalmaznak. Az első és a harmadik esetben ezek a számok Pozitívak, a további kettőben pedig Negatívak. Táblázatunk így biztosan tartalmaz annyi egymástól és a 0-tól különböző számot, amennyi a négyféle lehetséges Pi+Nj összeg maximuma.
A négy mennyiség összege 2(P1+P2+N1+N2)=4(k+n-4), így a négyük maximuma legalább ennek egynegyede, k+n-4, azaz a 0-val együtt most is létezik legalább n+k-3 különböző szorzat.
 

Vegyük észre azonban, hogy a négy mennyiség maximuma akkor lesz éppen az összegük egynegyede, ha mind a négy mennyiség egyenlő. Ez pedig esetünkben pontosan akkor igaz, ha P1=P2 és N1=N2, azaz k1=k2 és n1=n2. Ezek az egyenlőségek pedig csak úgy állhatnak fenn, ha k is és n is páratlan számok. Ebben az esetben viszont meg is adhatók az Ak és a Bn halmazok úgy, hogy a különböző szorzatok száma éppen n+k-3 legyen. Ehhez az szükséges, hogy a négy résztábla méretei egyenlők legyenek, az egyes résztáblákban ne legyen a minimálisnál több különböző szorzat, ezenkívül a két pozitív, illetve a két negatív résztábla ugyanazokat a szorzatokat tartalmazza.
Ez megvalósítható, ha
 

Ak={-2k-12,-2k-32,...,-2,0,2,...,2k-32,2k-12}és(*)Bn={-2n-12,-2n-32,...,-2,0,2,...,2n-32,2n-12}.


Így ha k>1 és n>1 páratlan számok, akkor m=n+k-3.
Ha viszont n és k közül legalább az egyik páros, akkor a Pi+Nj típusú összegek között vannak különbözők. Maximumuk ezért nagyobb, mint az összegük egynegyede, és így legalább n+k-3. Ebben az esetben tehát a 0-val együtt most is van legalább n+k-2 darab különböző az n⋅k darab szorzat között.
Eredményeinket összefoglalva a feladat kérdésére a következő választ adhatjuk:
 
1. Ha n=1 vagy k=1, akkor m=1;
 
2. ha n>1, k>1 és mindkettő páratlan, akkor m=n+k-3 azaz a létrejövő n⋅k szorzat között mindig van legalább n+k-3 különböző, és az Ak és a Bn halmazokat (*) szerint választva éppen ennyi;
 
3. ha n>1, k>1 és legalább az egyikük páros, akkor m=n+k-2, azaz a szorzatok között mindig van legalább n+k-2 különböző, és a 2/b ábra vizsgálatakor láttuk, hogy Ak és Bn megválasztható úgy, hogy a különböző szorzatok száma éppen ennyi legyen.