Feladat: F.2553 Korcsoport: 18- Nehézségi fok: átlagos
Füzet: 1986/április, 162 - 164. oldal  PDF  |  MathML 
Témakör(ök): Tengely körüli forgatás, Szabályos sokszög alapú gúlák, Derékszögű háromszögek geometriája, Egyenlő szárú háromszögek geometriája, Négyzetek, Szögfüggvények a térben, Szabályos sokszögek geometriája, Feladat
Hivatkozás(ok):Feladatok: 1985/november: F.2553

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Belátjuk, hogy a gúlacsúcsok valóban egy pontba forgathatók össze.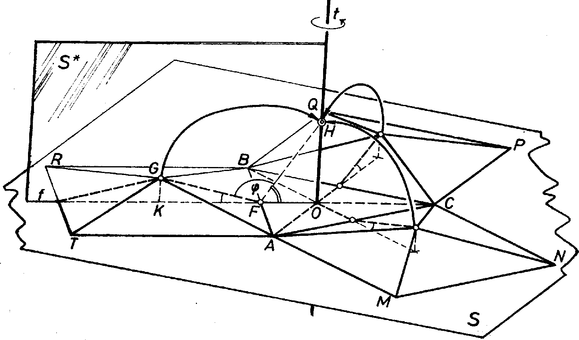
Jelöléseink: az ABC háromszög síkja legyen S, a háromszög középpontja O, az ABRT négyzet középpontja K, az ezen álló gúla négyélű csúcsa G, az AB alapél felezőpontja F, végül H az a pont, ahol a három gúla fő csúcsai egybeesnek (1.ábra).

 
 
1. ábra
 

Mivel GA=GB, azért G benne van az AB szakasz felező merőleges síkjában, S*-ban, amely egyben az RT alapélt is merőlegesen felezi. Továbbá GA=GT miatt G az AT, BR szakaszok közös felező merőleges síkjában is benne van, tehát G-nek S-en levő vetülete K.
Mialatt ezt a gúlát AB mint tengely körül forgatjuk, G és K az S*-ban fordulnak el, az F körüli köríveken. Ha S-et vízszintesen tartjuk, S* függőlegesen áll, mondhatjuk, hogy G az AB alapél S-beli f felező merőleges egyenese fölött halad. f egyben az ABC háromszögnek is tengelye, átmegy O-n, és így G eljuthat O fölé, ugyanis FO<FK<FG. Valóban az adatokból FO=FC/3=3/6=1/23, és FK=1/2, továbbá FG átfogó, FK pedig befogó az FGK derékszögű háromszögben.
Jelöljük a keresett oldalélt GA=x-szel, és a G által leírt körívnek O fölötti pontját H* gal. Ekkor a GAF és H*FO derékszögű háromszögek alapján
GF=x2-14,OH*=H*F2-FO2=GF2-112=x2-13.

Az ABC háromszög szabályos volta és a gúlák közös szerkesztési elve folytán az egész alakzat önmagába megy át az S-re O-ban állított t merőleges mint tengely körüli 120∘-os elfordítások útján. (A gúlákat természetesen egyformán S fölött gondoljuk.) Így a további két gúla csúcsa hasonlóan a BC, ill. CA alapél S-beli felező merőleges egyenese fölött mozog. Így a három főcsúcs csak a háromszög tengelyeinek közös O pontja fölött találkozhat, és az oldalélek közös x hossza alapján H*-ban valóban egybe is esnek.
Felírható x-szel kifejezve a szükséges forgatások közös φ nagysága:
φ=180∘-GFK∢-HFO∢,
ahol
cosGFK∢=12GF,cosHFO∢=123⋅HF.

2. Innen azonban egyelőre csak azt olvassuk ki, hogy a tovább vizsgálandó MN, PQ, RT alapélek a kívánt forgatások után S fölött egyenlő magasságban állnak meg, egy az S-sel párhuzamos S1 síkban lesznek. (A pontoknak a megállás utáni helyzeteit 1-es indexszel jelöljük.) Nyilvánvaló, hogy a létrejött M1N1P1Q1R1T1 szabályos hatszög O1 középpontja az S1 és t közös pontja, és hogy az oldalak közös hossza T1R1=T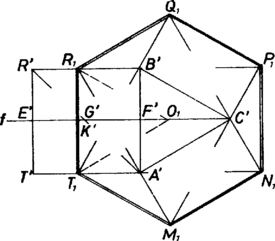R=AB=1 (2. ábra).
 
 
2. ábra
 

A kimondott szimmetria alapján elég vizsgálnunk a T1R1 oldalt. A TR él végpontjai az S*-gal párhuzamos síkokban fordulnak el A, ill. B körül, a T1R1-re merőlegesen álló egyenesek alatt, illetve fölött. Ha az első gúlát éppen 90∘-kal fordítjuk el, akkor TR az AB fölé jut. Ennek alapján hozzászerkeszthetjük a szabályos hatszöghöz az S-beli pontok S1-en levő vetületét: A' a T1-ben T1R1-re és M1-ben M1N1-re állított merőlegesek közös pontja, az O1T1M1 háromszög középpontja s í.t. másrészt T'A'=A'B'=1.
3. Megfordítva ezt, megkaphatjuk S-ben a gúlák megállított alapéleinek vetületét (3. ábra alsó része). R1, T1 vetületét R'1-vel, T'1-vel jelölve, ezek szimmetrikusak f-re, ezért R'1OF∢=R'1OT'1∢/2=360∘/12=BCO∢, tehát R'1 és T'1 az a pont, amely az OCB, ill. OCA háromszöget negyedik csúcsként parallelogrammává egészíti ki. Eszerint az RB alapél a B körüli elfordítás következtében a vetületben R'1B=OC=1/3-ra rövidült le, az elfordítás szögére 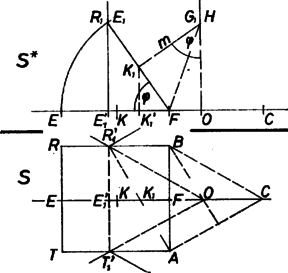cosφ=1/3.
 
 
3. ábra
 

4. Most már csak az S* síkban számolunk (3. ábra felső része). Ugyancsak 1/3 az ABRT négyzet EF=1 középvonalának E'F vetülete az EO egyenesre, ennélfogva a K1F=KF=1/2 szakasz vetülete K'1F=1/23, éppen egyenlő FO-val. Így K'1O=1/3, és ez a szakasz egyben K1H-nak, az első gúla K1G1=m tengelyének a vetülete az EO egyenesre. Mivel az OHK hegyesszög szárai merőlegesek az EFR1∢=φ száraira, azért
K'1O=msinφ=m⋅E1E'1E1F=m23=13,
amiből m=1/2, a gúlák tengelye egyenlő alapidomuk átlójának a felével.
Ez pedig azt jelenti, hogy a gúlák átlós síkmetszetében, pl. az ARG háromszögben G-nél derékszög van. A gúlák előállíthatók egységnyi élű szabályos oktaéderekből, valamelyik csúcstengelyük felező merőleges síkjával kettévágva, tehát a kérdéses oldalél hossza x=1.
Azt is kaptuk, hogy H egybeesik O1-gyel, az RTG lap R1T1G1 helyzete S1-ben van.
 

Megjegyzések. 1. A fenti megoldás 1. pontjának meggondolásait átléphettük volna ezzel az elterjedt ‐ szinte divatos ‐ szólammal: "szimmetriaokokból nyilvánvaló''. Szabad az ilyen kifejezés olyan dolgozatokban, ahol sokkal fontosabb dolgokról van szó, és az áthidalt rész tizedrangú sincs a mondanivalóhoz képest. (Egyébként a szimmetria nem ok, hanem magyarázat, megokolás.) Itt viszont éppen ez lett volna a gyakorolnivaló! A pontszámot azonban csak ott csökkentettük, ahol tévesen használták a szimmetriát, vagy más hiba akadt.
Gyakran mondta néhai Hajós György akadémikus: ha egy dolgozatban hibát gyanítunk, azt elsősorban a "nyilvánvaló''-k után keressük, és más efféle elnagyolásoknál.
Azért is részleteztük az 1. részt, mert itt a gúlák, a háromszög és a hatszög különböző szimmetriáiból állnak össze a kiindulási alakzat és a véghelyzet szimmetriái.
2. Az alakzat az 1983. évi brazíliai országos versenyen szerepelt abban a változatban, hogy GA=AB stb. Azt kellett bizonyítani, hogy a négyélű csúcsok egyesítése után szabályos hatszög keletkezik. Ott tehát eleve adva voltak a féloktaéderek.