| Feladat: | F.2552 | Korcsoport: 16-17 | Nehézségi fok: nehéz |
| Megoldó(k): | Batternay Anita , Benczúr A. , Bereczky Á. , Blahota I. , Bodor Sz. , Bóna M. , Bordás F. , Bozó A. , Deák Csaba , Dinnyés Enikő , Grallert Á. , Hajdú G. , Hantosi Zs. , Hartman Klára , Héjj T. , Horváth 572 L. , Illés A. , Istvanovszky M. , Kelemen Eszter , Kintli L. , Kiszel I. , Kocsis 443 Katalin , Ohnmach R. , Olasz-Szabó M. , Olláry P. , Pál G. , Pálmai L. , Ribényi Á. , Rung Éva , Weszelovszky Éva , Zóránd G. | ||
| Füzet: | 1986/április, 158 - 162. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Háromszögek hasonlósága, Vetítések, Kocka, Sokszögek szimmetriái, Szabályos sokszögek geometriája, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1985/november: F.2552 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás. 1. Jelöljük a szabályos hatszög oldalát -rel, középpontját -val, egymás utáni csúcsait -gyel, -vel, , -tal úgy, hogy az pont a oldalszakasz belső pontja, ha , és a szakasz belső pontja. Legyenek továbbá a leírás szerint keletkező háromszög csúcsai , , úgy, hogy az , egyenespár metszéspontja, az , páré, az , egyenespáré. Ekkor a feltevés szerint az félegyenesen van, ahol . Eleve kizárjuk, hogy -típusú pont egybeessék -típusú csúccsal, így az pontok egyértelműen létrejönnek.  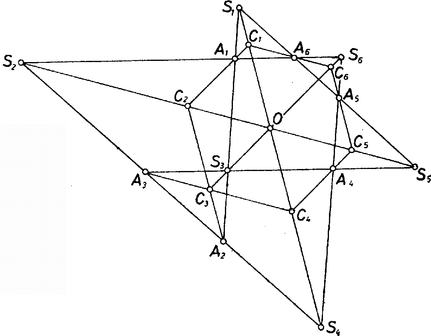 A feladat föltevése tulajdonképpen azt jelenti, hogy az csúcsok közül csak hármat választottunk szabadon, a további hármat már meghatározza, hogy , , egy-egy hosszú átló egyenesére esik. Például , és egyértelműen meghatározza az egész alakzatot: az egyenes kimetszi -ből -et, -ból -at, az egyenes -ből -öt és -ből -et, végül az egyenes -öt és -ot. Pontosabban: a , és szakaszokból kiszámítható egyrészt az , , pontok távolsága az illető hatszögoldal végpontjaitól, másrészt az , , csúcsok távolsága -tól és az ugyanolyan indexű csúcstól. Ezek után megkaphatjuk azoknak a pontoknak az -tól mért távolságát, ahol az egyenes az , félegyeneseket metszi, valamint az , egyenesek hasonlóan kiválasztott metszéspontjainak -tól mért távolságait. 2. Tekinthetnénk azonban az alakzatot úgy is, hogy az , , pontokat választottuk elsőnek, és e háromszög oldalai jelölték ki az pontokat a szabályos hatszög kerületén. Ebben a felfogásban jobban kihasználhatjuk a -hatszög szimmetriáját. Csak azt fogjuk igazolni, hogy az félegyenesnek -mal való metszéspontja azonos az -gyel való metszéspontjával. Mivel a hatszög az körüli -os elfordítással önmagába megy át, másrészt minden egyes pont szerepe is ugyanaz az alakzat kiépítésében, mint az és az ponté, azért és azonosságából az is következik, hogy az és félegyeneseken is egybeesik 2‐2 metszéspont. Rátérünk a tervbe vett számítás végrehajtására. Felhasználjuk, hogy a -hatszög 2‐2 alkalmasan választott oldala párhuzamos a bennük nem szereplő csúcsokat összekötő "hosszú'' átló egyenesével. 3. Az és , illetve az és hasonló háromszög párokból:
A jobb oldal első tényezője ‐ mint arány ‐ egyenlő az aránnyal, mert a és háromszögek megfelelő oldalegyenesei páronként párhuzamosak, ill. egybeesnek, a két háromszög hasonló. A második tényezőt a és , valamint és háromszögpárok hasonlósága alapján alakítjuk tovább: Mindhárom tényező átalakított kifejezésében csak az , , pontoknak az -tól, illetve a megfelelő -től való távolságai szerepelnek ‐ ezzel teljesen felhasználtuk az háromszög helyzetére vonatkozó föltevést ‐ és a szorzat értéke valóban 1. Evvel bebizonyítottuk az állításnak -re vonatkozó részét, és ebből ‐ mint előrebocsátottuk ‐ az -re, -ra vonatkozó része is következik. Az , , pontokról csak azt használtuk fel, hogy nem esnek egybe -val és az ugyanolyan indexű -vel, és hogy olyanok, hogy pl. és különbözők egymástól, és így -től is stb. Ennélfogva a feladat állítása minden ilyen megválasztású háromszögből keletkezett alakzatra is érvényes. (A 2.ábrán a hatszög belsejében van. Az érdeklődő számos másféle felvételt is kipróbálhat.) II. megoldás. A feladat állítását azáltal bizonyítjuk, hogy az ábra valamennyi vonalának egységes térbeli értelmezését adjuk. Első meglátásunk az, hogy a szabályos hatszög oldalainak és szóban forgó hosszú átlóinak együttese tekinthető egy kocka összes éle képének ‐ merőleges vetületének ‐ egy olyan síkon, amely merőlegesen áll a kocka egyik testátlójára. (Más szóval: a vetítés ezzel a testátlóval párhuzamosan történik.) 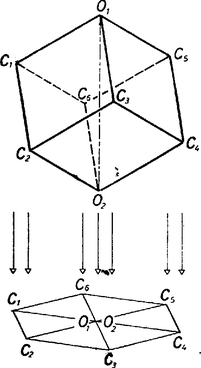 Az a két kockacsúcs, amelyik ezt a testátlót meghatározza, a vetületben egybeesik, ez ábránk pontja. Ha a kockán a testátló végpontjait -gyel és -vel jelöljük úgy, hogy az -ből kiinduló élek , , legyenek, akkor a kocka egy lapja , és az ezzel párhuzamos lapja ugyanúgy körüljárva . A térbeli hatszög minden egyes oldala kockaél, a síkbeli hatszög pedig a képnek "kontúrvonala''. A kocka még hátra levő három éle pedig -ben fut össze (3/a ábra). A feladatbeli alakzatnak a föltevésben és a bizonyítandó állításban szereplő 3‐3 egyenesét ezek után tekinthetjük egy sík által a kocka 6 lapsíkjából kimetszett egyenesek vetületének. A síkot meghatározza bármely olyan 3 pont az , valamint közül, amely nem esik egy egyenesbe. Vegyük úgy, hogy a síkot az -ből kifutó élek egyenesein levő , , pontjaival választottuk meg. Ekkor a föltevésbeli , és egyenesek metszésvonalai az -ben összefutó lapsíkokkal, sorra ezekkel: , és , továbbá sorra a , a , a él pontja (3/b ábra).  Így pedig a vizsgálandó egyenesek a síknak a további 3 kockalappal való metszésvonalai, hiszen és összekötése a lappal, és összekötése a lappal való metszésvonalat jelenti. E két egyenes metszéspontja mindkét lapsíkban benne van, tehát rajta van az él egyenesén, ez az , és ez éppen a bizonyítandó állítás első része. Ugyanígy adódik, hogy a további két metszéspont, , ill. rajta van az , ill. az él egyenesén. Ebben a felfogásban az hatszög szemben fekvő oldalának párhuzamos volta abból adódik, hogy a sík a kocka párhuzamos lapsíkpárjait párhuzamos egyenesekben metszi. Továbbá így elfajult eseteknek is értelmet tulajdoníthatunk, mint pl. -nek. Megjegyzések. 1. Könnyen adódik ezek után a feladat általánosítása: centrálisan szimmetrikus hatszöget venni a szabályos hatszög helyére. A 4. ábrán az a pont, amellyel az , , szakaszok a hatszöget 3 paralelogrammára darabolják, és ennek -ra való tükörképével ugyanez igaz az , , szakaszokra. (Itt a hatszög centruma.) Ha az , és egyenesek páronkénti , , metszéspontjai rendre rajta vannak az , , egyenesen, akkor az , , egyenesek páronkénti , , metszéspontjai rendre az , , egyenesen vannak.  Az I. megoldás számításai szinte betűről betűre átvehetők, mert ott a szabályosságból kizárólag bizonyos egyenesek párhuzamosságát használtuk ki, azok pedig itt is megvannak. ( mellé 1-es indexet kell tennünk.) A II. megoldás meggondolása is átvehető. A centrálszimmetrikus hatszög csúcsai és a 3‐3 paralelogrammára osztó , pontjai mindig tekinthetők egy paralelepipedon valamilyen irányú párhuzamos vetületének, a további egyenesek pedig a 6 lapsík és egy alkalmas metsző sík metszés vonalai vetületének. Itt már nem is kell értelmezést adni a vetítés irányára. 2. Eddig csak "könnyű'' példákat említettünk az -pontok és az , , pontok együttesének (illetve a síknak) 3 alkalmas képviselőjük által való meghatározására. A 4. ábrához kapcsolódva elmondunk egy kis "fogást'', amely célra vezet abban a "nehéz'' esetben, ha , és adottak, vagyis testeink három kitérő élének 1‐1 pontja. Tekintsük fedőlapnak az lapot és keressük meg ennek az egyenesen levő pontját. Azt ismerve, nyilván az egyenes metszi ki az , , pontokat. Mozgassunk gondolatban 1‐1 pontot az alapsíkbeli -ből és -ből egyenletesen úgy, hogy egyszerre érjenek -ba, majd tovább ugyanígy, míg elérik a fedősíkot. Így a két pont összekötő egyenese állandóan párhuzamos a egyenessel, az alap- és a fedősíkkal, tehát egyidejűen érkeznek -ba, ill. -be. Eszerint párhuzamos -tel. Vannak más nehéz esetek is! Az ilyen -ek révén emelkedik az típusú egyenesek "nevezetes'' pontjainak a száma. |