Kezdőlap


Feladat:	F.2505	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	1985/május, 208 - 210. oldal		PDF \| MathML
Témakör(ök):	Trigonometriai azonosságok, Euler-formula, Szabályos sokszög alapú gúlák, Egyenlő szárú háromszögek geometriája, Mértani sorozat, Térgeometria alapjai, Szabályos tetraéder, Szögfüggvények a térben, Feladat
Hivatkozás(ok):	Feladatok: 1984/december: F.2505

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a test csúcsainak, lapjainak, éleinek számát rendre $c, l, e$ -vel. Mivel a test konvex, azért minden háromszög minden oldala egy másik háromszög egy teljes oldalával alkot élt, csúcs nem lehet belső pontja élnek vagy lapnak. Érvényes a testre az Euler-féle poliéder-tétel: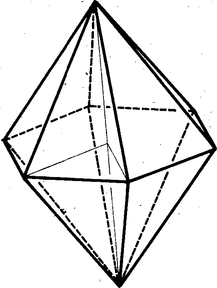

\begin{matrix} l + c = e + 2. \end{matrix}

Mivel minden lapnak

3

oldala van és minden él

2

laphoz tartozik hozzá, azért az éleket mindkét lapjukban beszámítva

\begin{matrix} 2 e = 3 l, azaz l = \frac{2 e}{3}, \end{matrix}

és a közlés szerinti mértani sorozat hányadosa

e / l = 3 / 2

. Ugyanennyi tehát

l / c

értéke is, vagyis

\begin{matrix} c = \frac{2}{3} l = \frac{4}{9} e . \end{matrix}

Ezeket az egyenletbe helyettesítve

e = 18, l = 12

és

c = 8

1. ábra

Ilyen testet kapunk, ha egy szabályos hatoldalú (egyenlő oldalélű) gúlát tükrözünk az alaplapjára (1. ábra). Az oldallapok vetülete az alaplap síkjára szabályos háromszög lesz, melynek oldala egyenlő a háromszöglapok alapjával, egyben a lapok szárának megrövidült vetületével. Ebben a testben tehát az egybevágó lapok szára nagyobb az alapjuknál, vagyis a szárak közti szög kisebb, mint

60^{\circ}

.
Kielégíti a feladat követelményeit a következő test is. Egy szabályos tetraéder lapjaira a középpontjukban merőlegest emelünk, ezekre kifelé egyenlő szakaszokat mérünk fel, és a végpontok adják a test további

4

csúcsát (2. ábra). Ezzel az eredeti

4

lapra egy-egy

3

oldalú gúlapalástot tettünk rá, az ezután látható lapok

(4 \cdot 3 = 12)

nyilvánvalóan egybevágó, egyenlő szárú háromszögek.

2. ábra

Ezekben a lapokban az alap a legnagyobb oldal, és a vele szemben levő szög kisebb, mint

120^{\circ}

, különben a gúlapalástok egy-egy síkot adnának. A szárak közti szögre alsó korlátot is kapunk a fölmérhető szakasz felső korlátjából.
Legyen az

A B C D

szabályos tetraéder

A B C

és

A B D

lapjának középpontja

D'

, ill.

C'

(a negyedik csúcs vetülete), az ezekben fölmért szakaszok végpontja

E

, ill.

G

, az

A B

él felezőpontja

F

. A konvexség követelménye, hogy

\begin{matrix} E F G ∢ = E F D' ∢ + D' F C' ∢ + C' F G ∢ = 2 \cdot E F D' ∢ + D' F D ∢ < 180^{\circ} \end{matrix}

legyen, vagyis

\begin{matrix} cos 2 \cdot E F D' ∢ > cos (180^{\circ} - D' F D ∢) = - \frac{1}{3}, \end{matrix}

hiszen

cos δ = cos D' F D ∢ = D' F / D F = 1 / 3

.
Tekintsük azt a

γ

szöget, amelyre

cos 2 γ = - 1 / 3

, vagyis amely mellett

A, E, B

és

G

egy síkban vannak. Ez nyilván hegyesszög, tehát

\begin{matrix} cos γ = + \sqrt[]{\frac{1 + cos 2 γ}{2}} = \frac{1}{\sqrt[]{3}} . \end{matrix}

Ebből

tg γ = \sqrt[]{2}

, így pedig

E F D' ∢ < γ

miatt

tg E F D' ∢ = D' E / D' F < 2

. És mivel még

D' F = C F / 3 = A B / 2 \sqrt[]{3}

, azért a fölmért szakaszra

\begin{matrix} D' E < \sqrt[]{2} D' F = \frac{1}{\sqrt[]{6}} A B = \frac{1}{2} D D' = \frac{2}{3} O D = \frac{2}{3} R, \end{matrix}

ahol

O

a tetraéder súlypontja, egyben középpontja, és

R

a körülírt gömb sugara.
Ha a merőlegesekre

D' E = 2 \cdot O D / 3

-at mérünk fel, akkor

O E = R

lesz, hiszen

O D' = D D' / 4 = O D / 3, E

rajta lesz a tetraéder köré írt gömbön, és a

8

csúcs kockát határoz meg.
Eredményünket így is kimondhatjuk: a test lapjain

90^{\circ} < A E B ∢ < 120^{\circ}

. ‐ A kristálytanban ezt az alakot triakisz-tetraédernek (

3

-szoros tetraédernek) nevezik.

Megjegyzések. 1. A feladat csak

1

megfelelő test leírását kérte, és a megoldást teljesnek tekintettük

1

test leírásával. Nekünk viszont nyilván mindkét testet le kellett írnunk.
2. Nem bizonyítjuk, hogy több ilyen test nem létezik, viszont megcáfolunk egy téves sejtést. Volt ilyen vélemény: megfelelő test az is, ha

6

háromszögből egy

6

-oldalú antiprizma palástját állítjuk össze, majd ennek szabályos háromszöget alkotó ,,bejáratai'' fölé

3

oldalú gúlapalástokat szerkesztünk (3. ábra, ilyen antiprizmát kapunk, ha egy lapjára állított szabályos oktaédert ,,függőlegesen'' nyújtunk vagy zsugorítunk). Ha azonban

A B H

és

A B F

egybevágó, egyenlő szárú háromszögek, akkor egyenlő szöggel hajlanak az

A B C

síkhoz (befelé, ill. kifelé) és a test 2-2 lapja síknégyszöggé áll össze;

A B

nem él lesz, hanem lapbeli átló. A testet

6

egybevágó rombusz határolná (paralelepipedon,

3

ütemű forgástengellyel,

3

szimmetriasíkkal. (Az antiprizma csúcsainak vetületei az

A B C

síkra egy szabályos hatszöget alkotnak!)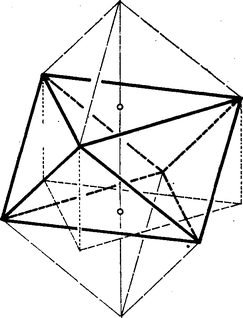

3. ábra