Feladat: F.2499 Korcsoport: 18- Nehézségi fok: átlagos
Megoldó(k):  Balogh 961 Cs. ,  Bán Rita ,  Bóna M. ,  Búza Kinga ,  Csermely Ágnes ,  Cynolter G. ,  Deák CS. ,  Dinnyés Enikő ,  Edvi T. ,  Grallert Ágnes ,  Hajdú S. ,  Hetyei Judit ,  Hornyák Z. ,  Horváth 572 L. ,  Íjjas Cs. ,  Karácsony P. ,  Králik B. ,  Limbek Cs. ,  Nyikes T. ,  Olasz-Szabó M. ,  Paál Beatrix ,  Pfeil T. ,  Werner P. ,  Zaránd G. 
Füzet: 1985/április, 158 - 160. oldal  PDF  |  MathML 
Témakör(ök): Vetítések, Térgeometriai bizonyítások, Tetraéderek, Szögfüggvények a térben, Feladat
Hivatkozás(ok):Feladatok: 1984/november: F.2499

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Keressük meg a B2 ponton át azt az S síkot, amely párhuzamos az állításbeli síkkal. Ekkor S tartalmazza a B2B1 egyenest. S csak úgy lehet párhuzamos C1C2-vel is ‐ ez az egyenes a tetraéder ADB=Sc lapsíkjában van ‐ , ha Sc-t a C1C2-vel párhuzamos egyenesben metszi.
Húzzuk meg tehát B2-n át (Sc-ben) a C1C2-vel párhuzamos egyenest és jelöljük DB-vel való metszéspontját E-vel, ekkor a keresett sík 3 pontja B1, B2 és E. És mivel az állításban szereplő harmadik egyenes, A1A2, a tetraéder BDC=Sa lapsíkjában van, azt kell csak belátnunk, hogy A1A2 és S-nek Sa-val való EB1 metszésvonala párhuzamosak.
Jelöljük a DA, DB, DC élek hosszát rendre a, b, c-vel és legyenek a D-nél az élek között levő szögek rendre BDC∢=α, CDA∢=β, ADB∢=γ. Ekkor szerkesztésünk folytán

DE=DC2DC1⋅DB2=cosαcosβbcosγ,DB1=bcosα,tehátDE:DB1=cosγ:cosβ=acosγ:acosβ=DA1:DA2,


és e sor két végén álló aránypárok egyenlősége éppen azt jelenti, amit bizonyítani akartunk.
 
 
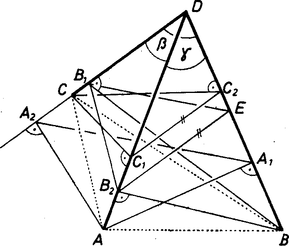1. ábra
 

Első ábránkon ‐ szokásosan ‐ a könnyebben elképzelhető esetre mutattunk példát, vagyis ha α, β, γ mindegyike hegyesszög. Ha tompaszög is van köztük, akkor modell készítése és a D-ben összefutó 3 lapnak mint palástnak síkba való kiterítése kevésbé könnyíti az elképzelést, mert egyes vetületek, esetleg mind a 6, az illető oldalél D-n túli meghosszabbítására esnek. Második ábránkon α-t és γ-t tompaszögnek gondoltuk és a testet majdnem fölülnézetből szemléltük, az alakzat hozzánk legközelebbi pontjai B1, B2, C2 és A1, ezek után hátrább következnek D, C1 A2 és E. (Az ABC háromszög oldalait el is hagytuk, nincs szerepük.)
 
 
2. ábra
 

Elveszti érdekességét, sőt a tartalmát is az állítás, ha az A1A2, B1B2, C1C2 egyenesek közül kettőnek közös az iránya, vagy ha valamelyik határozatlanná válik. Számításunk sem érvényes, ha csak egyik is 90∘ az α, β, γ közül. Például α=90∘ (és β≠90∘, γ≠90∘) esetén B1 és C2 egybeesik D-vel, tehát a B1B2 és C1C2 egyenesek egybeesnek DA-val (3. ábra, a DA él mentén felvágott palást kiterítése). Ha pedig α=β=90∘≠γ, akkor C1 és C2 egybeesik, összekötő egyenesük határozatlan. Ilyen esetben a DA és DB élt alkotó lapok derékszöget zárnak be. Ezeket az eseteket eleve kizárta a feladat szövege.
 
 
3. ábra
 

Megjegyzés. Elhangzott olyan vélemény, hogy az OKTV I. fordulójának egyik feladata * azonos a fenti feladattal. Az az igazság, hogy a forrás közös. Az valóban nem lényeges különbség, hogy ott olyan egyenes létezését kellett bizonyítani, amely bizonyos 3 egyenes mindegyikére merőleges, itt viszont egy síkét, amely 3 egyenes mindegyikével párhuzamos. De más-más egyenesek szerepelnek a folytatásban! A versenyfeladatban az egyes lapsíkokban önállóan keletkeznek a vetületeket összekötő a1b1, b2c2 és c3a3 egyenesek (jobb megkülönböztetés végett, a szokásostól eltérően kisbetűkkel idéztük, a 4. ábrán is így szerepelnek), míg a mi feladatunkban pl. A1A2 előkészítése, a vetítés, az ADB, ill. ADC lapsíkban történik, maga az egyenes pedig az A-val szemben levő BDC lapsíkban van.
 
 
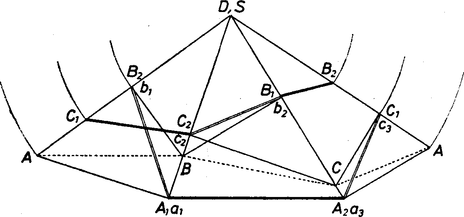4. ábra
 

Természetes tehát, hogy a feladatunkban szereplő sík nem azonos (és nem is párhuzamos) a versenyfeladatban szereplő merőleges síkkal. A 4. ábra egy tetraéderpalást kiterítésén szemlélteti a vizsgált 3‐3 egyenes különbözőségét. (Egymás után csatlakoznak az A1A2, a3c3, C1C2, c2b2, B1B2, b1a1 szakaszok, és a két végpont azonos.)
*"Az SABC tetraéderen az ASB, BSC és CSA háromszögek egyike sem derékszögű. Az ASB lap S csúcshoz nem tartozó magasságainak talppontja A1 és B1, hasonlóképpen a BSC lap S csúcshoz nem tartozó magasságainak talppontja B2 és C2, végül a CSA lap S csúcshoz nem tartozó magasságainak talppontja C3 és A3. Bizonyítsuk be, hogy van olyan egyenes, amely merőleges az A1B1, B2C2 és C3A3 egyenesek mindegyikére!''