|
| Feladat: |
F.2497 |
Korcsoport: 18- |
Nehézségi fok: átlagos |
| Megoldó(k): |
Balogh 961 Cs. , Bán Rita , Bodor Cs. , Bóna M. , Boros Z. , Csermely Ágnes , Csizmadia Gy. , Cynolter G. , Dinnyés Enikő , Fülöp T. , Gábor Z. Zs. , Grallert Ágnes , Hajdú S. , Hetyei Judit , Hornyák Z. , Horváth 572 L. , Karácsony P. , Kiszel I. , Kocsis 443 Katalin , Kónya Eszter , Kós Géza , Nyikes T. , Paál Beatrix , Pfeil T. , Ratkó Julianna , Regős G. , Ribényi Á. , Szabó 305 Gy. , Szalay Gy. , Szigeti Z. , Vajna M. |
| Füzet: |
1985/május,
198 - 203. oldal |
 PDF | PDF |  MathML MathML |
| Témakör(ök): |
Menelaosz-tétel, Egyenesek egyenlete, Négyszögek geometriája, Feladat |
| Hivatkozás(ok): | Feladatok: 1984/november: F.2497 |
|
|
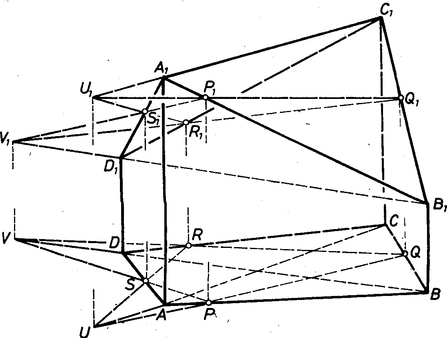
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás. Válasszuk a koordináta-rendszer és tengelyének a ill. átló egyenesét és jelöljük az első hat pont koordinátáit az alábbiak szerint: | |
A pont koordinátáit az (előjeles) aránnyal fejezzük ki -ból és -ből. Ezen az úton csak a , valamint eset nem jellemezhető, erre viszont az állítás úgyis semmitmondó.
Azt is tüstént kimondjuk, hogy pontjaink abszcisszái, valamint az ordináták is páronként különböznek egymástól és -tól.
Amíg az -tól -ig halad, növekedve minden pozitív értéket fölvesz, a -n túli meghosszabbításon és , ezért minden értéken átfut, -nek -n túli meghosszabbításán pedig és , végül is minden érték kiadódik. az egyenes végtelen távoli (ideális) pontját adná számára. Könnyű belátni, hogy az állítás olyankor is igaz.
A arány -nak és -nek a tengelyeken levő vetületeiben is megmarad: és innen
Mármost a egyenes iránytangense, majd egyenlete abból, hogy átmegy -n: | |
Hasonlóan a egyenes egyenlete , és ezekből koordinátái: | |
Hasonlóan a illetve egyenes egyenlete, majd koordinátái:
| |
Mielőtt továbbmennénk, rámutatunk az alakzatban mutatkozó szerepek szimmetriájára. Az ,,tengelyhez'' képest szimmetrikus szerepeket játszanak a következő pontpárok: | |
továbbá az és koordinátatengelyek, ezeknek megfelelően a koordináták párjai is, végül ezzel a ,,szereptükrözéssel'' Valóban, ilyen értelemben vett ,,párja'' | |
és ugyanígy és kifejezései is egymásba mennek át.
Hozzátesszük: ebben a szimmetriában a egyenes megfelelője , vagyis önmaga. Ekkor a feladat állítását így is kimondhatjuk: a és egyenesek metszéspontja azonos az és egyenesek metszéspontjával. Ehhez most már elég lesz kiszámítani és metszéspontját, majd megnézni, hogy véve az előzők szerinti párját, azaz és metszéspontját, a két pont azonos-e egymással.
Jelöljük -nek -n és -n levő pontját -rel, ill. -gal.
iránytangense céljára abszcisszáik különbsége így alakítható: | |
tehát egyenlete: | |
A egyenes egyenlete: tehát
Kiszámítjuk -ből -ot a fentebb mondott ,,tükrözéssel'': | |
ez pedig azonos kifejezésével. Ezzel az állítást bebizonyítottnak tekintjük.
II. megoldás. Segédtételül felhasználjuk Menelaosz-tételét: ha az háromszög és oldalegyenesein levő , ill. , ill. pontokra fennáll a következő egyenlőség: | |
akkor az pontok egy egyenesen vannak. A tétel megfordítása is igaz.
A szakaszok előjellel együtt értendők, pozitívnak véve pl. az körüljárás irányát. A segédtételt alkalmazva az I. megoldás jelöléseivel a háromszögre és az egy egyenesen sorakozó pontokra: a háromszögre és az pontokra, majd beírva (1.1) eredményét: | | (1.2) |
továbbá az háromszögre és a pontokra (vagyis az (1.1) eset háromszöge és egyenese helyére a ,,tükörképeket'' véve): végül ugyanígy az háromszögre és az pontokra: | | (2.2) |
Az utóbbi két sor eredménye is kiadódik tükrözéssel az előbbi két sor eredményeiből.
Ezek szerint, kellő átrendezést végezve tehát azonos -rel; ezzel a bizonyítást befejeztük.
Itt nem használtuk ki, hogy és merőlegesek egymásra, ennélfogva ez a rész a feladat föltevéseiből elhagyható.
III. megoldás. Itt sem használjuk ki és merőleges voltát. Ha a és egyenlőségek közül egy vagy több teljesül, akkor vagy nincs értelme a keresett metszéspontnak, vagy az triviálisan , illetve . Ha , akkor a két egyenes egybeesik. Elég tehát azt az esetet vizsgálni, amikor ezek nem állnak fenn.
Segítségül veszünk olyan és nem egy síkba eső pontokat, amelyeknek merőleges vetülete a feladat síkjára sorra és . Legyen az az és a egyenes azon pontja, amelynek vetülete illetve . és egyenesek -ben metszik egymást, tehát egy síkban van ez a négy pont, és így és egyenes is egy síkban van. Nem párhuzamosak, mert vetületeik -ban metszik egymást. Ezért van egy metszéspontjuk, és ennek vetülete . ‐ Hasonlóan látható, hogy egy síkban van, azaz és metszi egymást -ben, amelynek a vetülete.
Elég lenne belátni, hogy az és egyenesek egy ponton mennek át, mert akkor ez igaz a vetületeikre is. Először is belátom, hogy páronként egy síkban vannak, de nincs mind egy síkban. Valóban, és benne van és síkjában, és benne van és síkjában, és pedig benne van és síkjában (három pont mindig egy síkban van). De ha mind egy síkban lennének, akkor ebben lenne a egyenes pontja és az egyenes pontja is, csakhogy nem voltak egy síkban. Elég tehát belátni, hogy 3 egyenes, közül; ha bármely kettő egy síkban van, akkor egysíkúak, párhuzamosak, vagy egy ponton mennek át. Ekkor ugyanis a vetületek, vagy mind párhuzamosak, vagy létezik a metszéspont, és rajta van -n.
Legyen három ilyen egyenes ! Ekkor bármely kettő vagy metszi egymást, vagy párhuzamos. Három eset van: a) mind párhuzamos, b) kettő párhuzamos, a harmadik metszi őket, de ekkor benne van a síkjukban, c) páronként metszik egymást. Így vagy egy háromszög oldalegyenesei, tehát egysíkúak, vagy a három metszéspont egybeesik, és ezen a ponton megy át mindhárom egyenes. ‐ Ezzel a megoldást befejeztük.
Megjegyzés: A feladat lényegében ekvivalens Desargues tételével: ha két háromszög olyan helyzetű (a síkban vagy a térben), hogy egy-egy megfelelő szögpontjukat összekötő egyenesek egy ponton mennek át (vagy ha a egyenes párhuzamos egymással), akkor a megfelelő oldalegyenesek metszéspontjai egy egyenesen vannak. A tétel megfordítása is igaz, nálunk: a és háromszögek megfelelő oldalegyenespárjainak metszéspontjai , ezért a megfelelő csúcspárok összekötő egyenesei -ben metszik egymást.
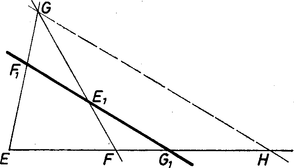
Mi a megfordítást igazoljuk a párhuzamos szelők tételeinek kétszeri alkalmazásával: ha egy egyenes az oldalegyeneseket az -es indexű pontokban metszi, akkor fennáll szakaszból képezett szorzatok közti egyenlőség, a jobb oldalt ellentett jellel véve.
Húzzuk meg -n át az -vel párhuzamos egyenest és jelöljük -fel való metszéspontját -val.
Ekkor
| |
amiből, egyes szakaszokat -gyel szorozva és egyben irányukat megfordítva
végül szorzással, egyszerűsítéssel az állítást kapjuk. ‐ Akkor is érvényes az egyenlőség, ha átmegy valamelyik csúcson. |
|
 PDF |
PDF |  MathML
MathML