Feladat: F.2485 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Bíborka Judit 
Füzet: 1985/március, 112 - 113. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek hasonlósága, Trapézok, Paralelogrammák, Párhuzamos szelők tétele, Párhuzamos szelők tételének megfordítása, Feladat
Hivatkozás(ok):Feladatok: 1984/szeptember: F.2485

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. a) Húzzuk meg a BD átlóval párhuzamos egyenest Q-n és P-n át, és messe ez a CD, ill. AB egyenest 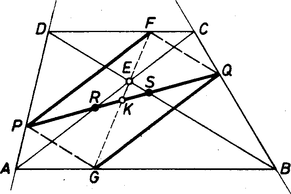F-ben, ill. G-ben.

 
 
1. ábra
 


Ekkor a párhuzamos szelők tétele és a föltevés szerint
CFFD=CQQB=APPD=k.
Ennélfogva ugyanezen tétel megfordítása szerint PF||AC, továbbá ugyanígy QG||AC. Ezek szerint a PFQG négyszög paralelogramma, és AG:GB=k.
Jelöljük az átlók metszéspontját a paralelogrammában K-val, az eredeti trapézban E-vel. ECD és EAB az E centrumra nézve hasonló helyzetű háromszögek, csúcsaik a felsorolás rendjében felelnek meg egymásnak, ennélfogva F és G pontjaik is egymás megfelelői. Ezért az FG átló E-n is átmegy.
Így pedig a PFQ és RES háromszögek K-ra mint centrumra nézve hasonló helyzetűek. Mivel K felezi PQ-t, azért az RS szakaszt is felezi, tehát R és S a PQ egyenesen K-ra nézve szintén szimmetrikus helyzetű pontok, és így PR=QS. Ezt kellett bizonyítanunk.
Ha CD=AB, akkor P és Q egymás tükörképei E-re, ekkor R és S egybeesik E-vel.
b) Ha P az AD szakasz valamelyik meghosszabbításán van, akkor az AP és PD szakaszok ellentétes irányúak, tehát az AP:PD=k arány értéke negatív lesz. És pedig amint P az A-n túl távolodik, k a 0-tól szigorúan monoton csökken, de nem éri el a (-1)-et, ha pedig D-n túl távolodik P, akkor szigorúan monoton nő, de nem éri el a (-1)-et. Emiatt a föltételezett egyenlőség szerint Q a C-n, ill. B-n túli meghosszabbításon lesz. Megmarad, hogy A és C egymás megfelelői E-re nézve, ugyanúgy B és D is, így pedig bizonyításunk betűről betűre érvényes marad. Ha speciálisan P-t A-ban választjuk, akkor Q a C-ben lesz, ugyanígy egy megfelelő helyzet P,Q-ra D és B, de ilyenkor az állításnak nincs tartalma, mert R és S egyike határozatlan.
 

II. megoldás. Mindjárt azt látjuk be, hogy az állítás az AD egyenes tetszőleges P pontjára igaz, ha az arányokat előjellel együtt értjük. Láttuk az I. megoldás b) részében, hogy az így vett arány értéke egyértelműen meghatározza az R, illetve S pont helyzetét a PQ egyenesen is, ezért a következő egyenlőséget bizonyítjuk: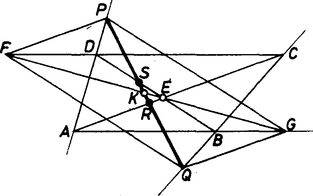
PRRQ=QSSP.

 
 
2. ábra
 

Így R és S a PQ szakasz felezőpontjára nézve tükrös pontok, amiből az állítás következik.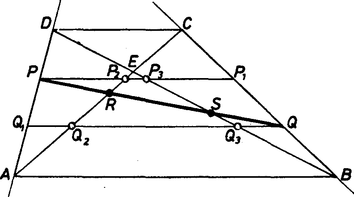
 
 
3. ábra
 

Húzzuk meg a párhuzamosokat AB-vel P-n és Q-n át, és jelöljük a szemben levő szárra való metszéspontjukat P1-gyel, ill. Q1-gyel, továbbá AC-vel és BD-vel való metszéspontjukat P2, P3-mal, ill. Q2, Q3-mal (3. ábra).
Az SPP3 és SQQ3 hasonló háromszögekből, majd a DPP3, DAB és a BQQ3, BCD párokból
SPSQ=PP3QQ3=AB⋅DPDACD⋅BQBC=ABCD⋅BCBQDADP=ABCD⋅1+CQQB1+APPD=ABCD,
egyenlő a trapéz párhuzamos oldalainak arányával. E bizonyításban P, Q, A, B, C, D helyére sorra P, Q, C, D, A, B-t írva és a 3-as indexek helyére 2-est, S helyére R-et,
RPRQ=DCAB=1:SPSQ,
és ezt akartuk bizonyítani.
Nem létezik a felhasznált SPP3 és SQQ3 háromszög, illetve RPP2 és RQQ2, ha a két segédpárhuzamos egybeesik. Ekkor azonban P és Q nyilvánvalóan felezik a szárakat, a föltételbeli arányok közös értéke 1, és az állítás szinte semmitmondó.
Eredményünk így is kimondható : mialatt P az AD száregyenesen halad, és Q a CB egyenesnek az aránypár által meghatározott pontja, az SP/SQ és az RQ/RP arányok értéke közös állandó, nem függ P helyzetének megválasztásától.