Kezdőlap


Feladat:	F.2439	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	1984/március, 109 - 111. oldal		PDF \| MathML
Témakör(ök):	Trigonometriai azonosságok, Szabályos sokszög alapú gúlák, Hossz, kerület, Szögfüggvények a térben, Feladat
Hivatkozás(ok):	Feladatok: 1983/október: F.2439

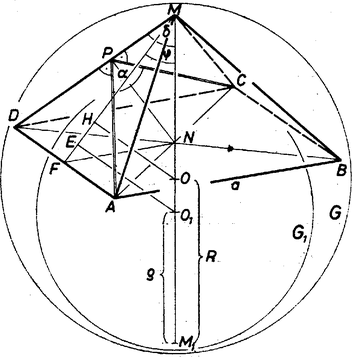
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Jelöljük az $A B C D M$ szabályos $4$ -oldalú gúla alapnégyzetének középpontját $N$ -nel, az $A D$ alapél hosszát $a$ -val, felezőpontját $F$ -fel, továbbá a körülírt $G$ és a kérdéses $G_{1}$ gömb középpontját és sugarát $O$ -val, $R$ -rel, illetve $O_{1}$ -gyel és $ϱ$ -val, végül az adott lapszöget $α$ -val, az $F M O$ szöget $φ$ -vel, a $D M O$ szöget $δ$ -val.
A gúla szimmetrikus egyrészt a $D M O = S$ , másrészt az $F M O = S_{1}$ síkra. Az utóbbi merőleges az $A D M = L$ oldallapsíkra. Az $S_{1}$ -re való tükrözés egymásba viszi át az $A D$ csúcspárt és önmagába az egész alakzatot, tehát $G_{1}$ -nek a $G$ -vel és az $L$ -lel való $M_{1}$ , ill. $E$ érintkezési pontját is. Ezért $E$ rajta van $L$ és $S_{1}$ metszésvonalán, az $M F$ egyenesen, $M_{1}$ pedig $G$ -nek $M$ -mel átellenes pontja, továbbá az $O_{1}$ is az $M O$ -n van.
Az $O_{1} E M$ derékszögű háromszögben

\begin{matrix} sin φ = \frac{O_{1} E}{M O_{1}} = \frac{O_{1} E}{M M_{1} - O_{1} M_{1}} = \frac{ϱ}{2 R - ϱ}, \end{matrix}

innen

\begin{matrix} ϱ = \frac{2 R}{\frac{1}{sin φ} + 1} . \end{matrix}

(1)

Legyen

A

vetülete az

M D

egyenesen

P

, az

S

-re való tükrösség alapján ez egyben

C

-nek is vetülete, tehát

A P C ∢ = α

. Az

A P C

egyenlő szárú háromszögből

\begin{matrix} ctg \frac{α}{2} = \frac{P N}{A N} = \frac{P N}{D N} = sin N D P ∢ = cos δ . \end{matrix}

(2)

(1) céljára

φ

és

δ

közt kapunk összefüggést:

\begin{matrix} tg φ = \frac{F N}{M N} = \frac{D N}{\sqrt[]{2} M N} = \frac{1}{\sqrt[]{2}} tgδ, \end{matrix}

(3)

továbbá

2 R

és az ismert

A D = a

alapél között a

D M M_{1}

derékszögű háromszögből:

\begin{matrix} 2 R = \frac{D M}{cos δ} = \frac{D N}{cos δ sin δ} = \frac{a}{\sqrt[]{2} cos δ sin δ} . \end{matrix}

(4)

Egyelőre ott tartunk, hogy numerikus adatok mellett

α

-ból (2) alapján kiszámíthatjuk

δ

-t, ebből (3) alapján

φ

-t és (4) alapján

2 R

-et ‐ az

a

élt is felhasználva ‐ és ekkor (1)-ből kiszámítható a

ϱ

sugár.
A következőkben

ϱ

-t közvetlenül

a

-val és

α

-val fogjuk kifejezni. Egyfelől

\begin{matrix} sin δ = \sqrt[]{1 - cos^{2} δ} = \sqrt[]{1 - {ctg}^{2} \frac{α}{2}} = \sqrt[]{1 - \frac{1 + cos α}{1 - cos α}} = \sqrt[]{\frac{- 2 cos α}{1 - cos α}}, \end{matrix}

így a (4)-beli nevező

\begin{matrix} \sqrt[]{\frac{2 (1 + cos α)}{1 - cos α} \cdot \frac{- 2 cos α}{1 - cos α}} = \frac{2 \sqrt[]{- cos α (1 + cos α)}}{1 - cos α}, \end{matrix}

továbbá az (1)-beli nevező céljára

\begin{matrix} \frac{1}{sin φ} = \sqrt[]{\frac{1 + {tg}^{2} φ}{{tg}^{2} φ}} = \sqrt[]{\frac{2}{{tg}^{2} δ} + 1} = \sqrt[]{\frac{2 cos^{2} δ}{1 - cos^{2} δ} + 1} = \sqrt[]{\frac{cos^{2} δ + 1}{1 - cos^{2} δ}} = \\ = \sqrt[]{\frac{{ctg}^{2} \frac{α}{2} + 1}{1 - {ctg}^{2} \frac{α}{2}}} = \sqrt[]{\frac{1}{- cos α}}, \end{matrix}

ennélfogva (1)-ből

\begin{matrix} ϱ = \frac{a (1 - cos α)}{2 \sqrt[]{1 + cos α} (1 + \sqrt[]{- cos α})} . \end{matrix}

Az adott

α

mindig tompaszög, tehát

- cos α > 0

, ugyanis rögzített

R

mellett, ha

N

tart

M

-hez, akkor

α

tart

180^{\circ}

-hoz. Ha pedig

N

M_{1}

-hez tart, akkor

α

tart

90^{\circ}

-hoz.
2. Az előírt speciális esetben gúlánk egy szabályos oktaéder fele,

N

egybeesik

O

-val. Ekkor az oldallapok

M F N ∢ = α / 2

szöggel hajolnak az alapsíkhoz:

\begin{matrix} cos \frac{α}{2} = \frac{a / 2}{a \sqrt[]{3} / 2} = \frac{1}{\sqrt[]{3}}, cos α = 2 cos^{2} \frac{α}{2} - 1 = - \frac{1}{3} \end{matrix}

és

\begin{matrix} ϱ = \frac{a}{\sqrt[]{2}} (\sqrt[]{3} - 1) = R (\sqrt[]{3} - 1) . \end{matrix}

3. Belátjuk még, hogy ha

90^{\circ} < α < 180^{\circ}

, akkor mindig létezik a

G_{1}

gömb, illetve az

O M_{1}

szakasz megfelelő belső

O_{1}

pontja. Tekintsük

O

-nak

H

vetületét az

M F

félegyenesen, ekkor

O H = R sin φ < R = O M_{1}

, tehát az

O

körüli, a gúla oldallapsíkjait érintő gömb nem érinti

G

-t. Amint egy

O_{1}^{*}

pont halad

O

-tól

M_{1}

-ig,

O_{1}^{*} H^{*}

monoton és folytonosan nő,

O_{1}^{*} M_{1}

pedig folytonosan csökken

O

-ig, tehát közben pontosan egyszer beáll az

O_{1}^{*} H^{*} = O_{1}^{*} M_{1}

egyenlőség.