Kezdőlap


Feladat:	F.2438	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1984/február, 66 - 67. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Ellenpélda, mint megoldási módszer a matematikában, Feladat
Hivatkozás(ok):	Feladatok: 1983/október: F.2438

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Elég egyetlen ellenpélda, hogy nemet mondhassunk a kérdésre. Legyen $A B C$ derékszögű háromszög, csúcsaiban sorra $30^{\circ}$ -os, $90^{\circ}$ -os, $60^{\circ}$ -os szöggel és kapcsoljuk ehhez negyedik csúcsnak azt a $D$ pontot, amelyre $D C ∥ A B$ és $D B ⊥ A C$ . A négy részre vágott $A B C D$ trapéznak az $A B$ , $B C$ , $C D$ oldalra támaszkodó részeiben a szögek ismét $30^{\circ}$ , $60^{\circ}$ , $90^{\circ}$ -osak. Az $A D$ -re támaszkodó háromszögben viszont nincs $60^{\circ}$ -os szög, amely egyedül felelne meg az állításnak, ugyanis $D$ nem tükörképe a $B$ -nek az $A C$ átlóra nézve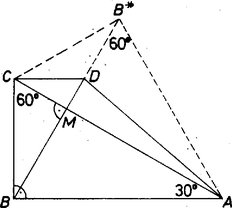

\begin{matrix} C D \neq C B (= \sqrt[]{3} C D) \end{matrix}

miatt.

1. ábra

2. Van olyan négyszög, amely alapot ad a föltett kérdéshez. Legyen

A B C D

olyan trapéz, amelyben

B

-nél derékszög van,

B C = A B / \sqrt[]{2}

és

C D = B C / \sqrt[]{2}

. Ebben

cos C A B ∢ = \sqrt[]{2 / 3}

, másfelől

cos A D B ∢ = \frac{1}{3}

, és a

cos 2 x = 2 cos^{2} x - 1

azonosság szerint

cos 2 \cdot C A B ∢ = 1 / 3

.
3. Nincs másfajta konvex négyszög, amely megfelelne a feladatban szereplő feltételeknek, mint azok a derékszögű trapézok, amelyekben az átlók

M

metszéspontjánál derékszögek vannak, és a két alap különböző hosszú. Ha ugyanis az

M

-nél keletkező csúcspárok közül kettőnek a nagysága

γ \neq 90^{\circ}

, akkor a másik kettőé

180^{\circ} - γ

, és az ezeket tartalmazó háromszögekben nem lehet

γ

nagyságú szög, hiszen a további két szög együttvéve

γ

.
Ha pedig

A C ⊥ B D

, és azt kívánjuk, hogy az

A B M

B C M

és

C D M

háromszögek hasonlóak legyenek valamilyen körüljárás szerint, akkor

A B M ∢ = β \neq 45^{\circ}

jelöléssel a

C B M

szögre a

90^{\circ} - β

és a

β

értékek jönnek szóba.

2. ábra

Az első esetben

A B C ∢ = 90^{\circ}

, a másodikban az

A B C D

négyszög deltoid lesz, a megkülönböztetett

D A M

háromszög egybevágó a

D C M

-mel, mi pedig nem ezt keressük. Ugyanide vezetne a

β = 45^{\circ}

föltételezés is.
Folytatva az első esetet, ismét nem lehet

B C M ∢ = D C M ∢

, tehát

B C M ∢ + D C M ∢ = 90^{\circ}

C

-nél is derékszög van, és így

C D ∥ A B

C D M ∢ = β

.
Végül

β \neq 45^{\circ}

miatt elég tekintenünk a

β > 45^{\circ}

esetet. Ekkor

A M > B M > C M > D M

és ez a négy szakasz mértani sorozatot alkot (ebben a sorrendben), melynek hányadosa

0 < ctg β < 1

, így

A D M ∢ = {ctg}^{3} β

, ezért

\begin{matrix} 45^{\circ} < β < A D M ∢ . \end{matrix}

A D M ∢ = 2 (90^{\circ} - β)

feltételezés a már látott

ctg β = \sqrt[]{2}

esetre vezet.