| Feladat: | F.2435 | Korcsoport: 16-17 | Nehézségi fok: nehéz |
| Megoldó(k): | Németh-Buhin Ákos | ||
| Füzet: | 1984/április, 155 - 157. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Geometriai egyenlőtlenségek, Terület, felszín, Szélsőérték-feladatok differenciálszámítás nélkül, Számtani-mértani egyenlőtlenségek, Feladat, Síkgeometriai számítások trigonometriával | ||
| Hivatkozás(ok): | Feladatok: 1983/október: F.2435 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás. Jelöljük -rel a kör sugarát, és legyen egy -t érintő háromszög. Belátjuk, hogy
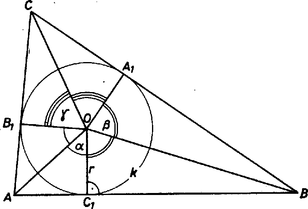 Az és háromszögek egybevágóak, hiszen -nél, ill. -nél derékszög van, és . Következésképp , jelöljük ezt a szöget -val. Hasonlóan látható, hogy és , jelöljük e szögeket -val, ill. -val. Az derékszögű háromszögben , amiből következik. Ugyanígy és . Ezeket (1)-be írva végül is azt kell igazolnunk, hogy
A négyzetes és harmonikus közép közötti összefüggés alapján:
Egyenlőség akkor áll, ha egyrészt , másrészt ha , tehát (2)-ben is pontosan akkor áll egyenlőség, amikor . Ez esetben az háromszög szabályos, amit bizonyítani kellett. II. megoldás. Jelöljük a kör sugarát -rel, az háromszög oldalait , , -vel, és legyen a szokásos módon . Ekkor a háromszög területe egyrészt , másrészt a Heron-képlet alapján , azaz
(4)-et felhasználva kapjuk, hogy Megjegyzés. A dolgozatokban sokféle megoldástípus fordult elő, nagy részük nem is volt helyes. A hibás dolgozatok jelentős részében az a helytelen következtetés található, hogy mivel a számtani (ill. négyzetes) és mértani (ill. harmonikus) közepek közti egyenlőtlenségben egyenlőség akkor és csak akkor áll fenn, ha a számok egyenlők, ezért a számtani (ill. négyzetes) közép minimuma is ekkor van. Másik gyakori hiba, hogy a négyzetösszeget tagonként minimalizálják. Sokszor előfordult az is, hogy a kör helyett az háromszöget rögzítették és keresték azt a pontot, amire minimális. |