Kezdőlap


Feladat:	F.2419	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Simon Péter
Füzet:	1983/november, 129 - 130. oldal		PDF \| MathML
Témakör(ök):	Egyenes, Koszinusztétel alkalmazása, Ellipszis, mint mértani hely, Feladat
Hivatkozás(ok):	Feladatok: 1983/április: F.2419

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a $C$ -ből induló belső szögfelező és $A B$ metszéspontja 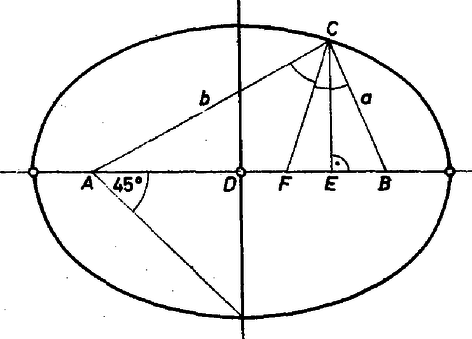$F$ .

Ekkor a szokásos jelölésekkel

A F + F B = c

, és a szögfelezőre vonatkozó ismert tétel alapján:

\begin{matrix} A F : F B = A C : C B = b : a . \end{matrix}

Ezekből

A F = c \cdot b / (a + b)

.
Az általánosság korlátozása nélkül feltehetjük, hogy

a \leq b

, így

D F = A F - \frac{c}{2} = c \frac{b - a}{2 (a + b)}

. A cosinustétel alapján:

cos A B C ∢ = \frac{a^{2} + c^{2} - b^{2}}{2 a c}

, ezért

D E = \frac{c}{2} - a \cdot cos A B C ∢ = \frac{b^{2} - a^{2}}{2 c}

.
Azon

C

pontok mértani helyét keressük, melyekre

\begin{matrix} \frac{D E}{2} = D F, \end{matrix}

vagyis

\begin{matrix} \frac{b^{2} - a^{2}}{4 c} = c \frac{b - a}{2 a + b}, \end{matrix}

Átrendezve:

\begin{matrix} (b - a) [{(2 a + b)}^{2} - 2 c^{2}] = 0. \end{matrix}

Ez akkor és csak akkor teljesül, ha vagy

a = b

, vagy

a + b = \sqrt[]{2} c

Az első esetben a háromszög egyenlő szárú,

D

és

E

egybeesik. A mértani hely az

A B

szakasz felező merőlegese, kivéve a

D

pontot, hiszen ha

C

A B

egyenesre esik, nincs háromszög, nincs szögfelező.
A második egyenlet az

a \leq b

feltétellel együtt

\sqrt[]{2} c

nagytengelyű,

A

B

fókuszú ellipszisnek

B

-hez közelebbi felét adja.
Megengedve az

a > b

esetet is, ugyanehhez az összefüggéshez jutunk, és megkapjuk az ellipszis másik ívét.
A gondolatmenetet megfordítva belátható, hogy az ellipszis minden pontja, az

A B

-vel közös két pontját kivéve, hozzátartozik a mértani helyhez.

Simon Péter (Bp., József Attila Gimn., III. o. t.)