Kezdőlap


Feladat:	F.2409	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Alexy N. , Balázs Judit , Bán Rita , Bartha M. , Böröczky L. , Csillag P. , Danyi P. , Derekas Edit , Erdős 228 L. , Herendi T. , Hetyei G. , Hraskó A. , Ilosvay F. , Kakuk Ildikó , Kerner Anna , Kovalscsik I. , Ladányi L. , Lengyel Zs. , Megyesi G. , Pásztor J. , Peták T. , S. Fülöp T. , Simon J. , Simon P. , Szabó 112 T. , Szemők Á. , Szirmai J. , Szlovák Judit , Szöllősi Gabriella , Vindics I. , Zemplényi K. , Zsigri G.
Füzet:	1983/október, 61 - 63. oldal		PDF \| MathML
Témakör(ök):	Gúlák, Gömb és részei, Feladat, Térelemek és részeik
Hivatkozás(ok):	Feladatok: 1983/február: F.2409

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Tegyük fel, hogy az $A B C$ alapon álló $A B C D$ gúlába sikerült beilleszteni az $R$ sugarú $G_{i}$ gömböket a követelményeknek megfelelően ( $i = 1, 2, 3$ ) úgy, hogy az $A B D$ oldallapot $G_{1}$ és $G_{2}$ érinti, a $B C D$ lapot $G_{2}$ és $G_{3}$ , végül $C A D$ -t a $G_{3}$ és $G_{1}$ . Jelöljük $G_{i}$ középpontját 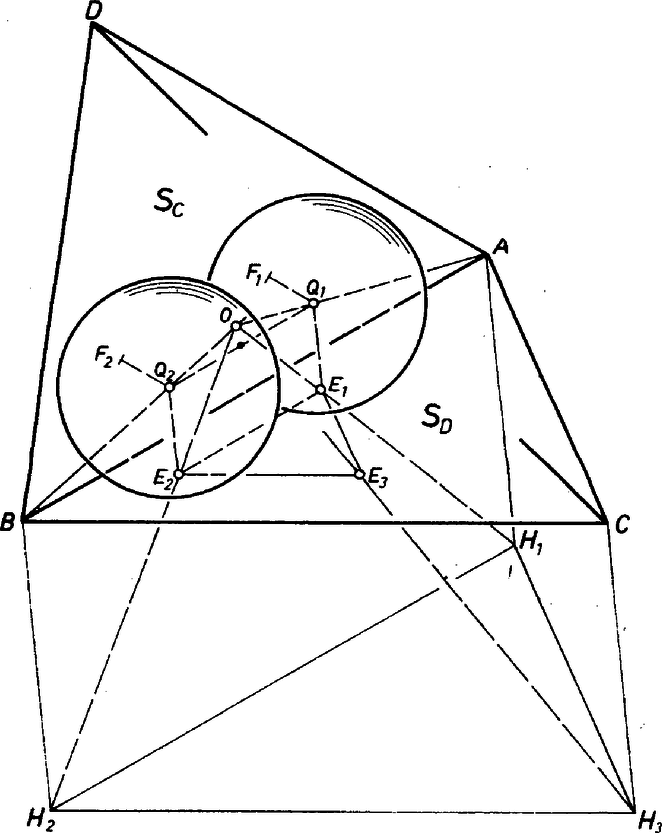$Q_{i}$ -vel.

Q_{1}

Q_{2}

Q_{3}

pontok mindegyike

R

távolságra van az

A B C

háromszög

S_{D}

síkjától, ennek a síknak ugyanarra a partjára esik, tehát a

Q_{1} Q_{2} Q_{3}

háromszög síkja párhuzamos az

S_{D}

síkkal. S mivel a gömbök páronként érintik egymást, a

Q_{1} Q_{2} Q_{3}

háromszög mindegyik oldala

2 R

, a háromszög szabályos.
Megmutatjuk, hogy az

A B C

háromszög ugyancsak szabályos, ez tehát szükséges feltétele annak, hogy a gömbök beírhatók legyenek a gúlába. Nyilván elég például azt belátni, hogy a

Q_{1} Q_{2}

egyenes párhuzamos az

A B

alapéllel.
Legyen

G_{i}

érintési pontja az alapsíkon

E_{i}

, továbbá az

A B D = S_{C}

síkon

F_{i} (i = 1, 2)

. Mivel

Q_{1} E_{1} = Q_{2} E_{2} = R

, és

Q_{1} E_{1}

Q_{2} E_{2}

merőleges

S_{D}

-re, azért a

Q_{1} Q_{2}

egyenes párhuzamos

E_{1} E_{2}

-vel. Megfordítva:

S_{D}

-ben az

E_{1} E_{2}

-vel párhuzamos egyenesek ‐ és csak ezek ‐ párhuzamosak

Q_{1} Q_{2}

-vel. Ugyanígy

S_{C}

egyenesei közül az

F_{1} F_{2}

-vel párhuzamosak ‐ és csakis ezek ‐párhuzamosak

Q_{1} Q_{2}

-vel. Ámde

S_{D}

-nek és

S_{C}

-nek egyetlen közös egyenese van, az

A B

élegyenes, ez tehát párhuzamos

Q_{1} Q_{2}

-vel (és

E_{1} E_{2}

-vel,

F_{1} F_{2}

-vel is). ‐ Ezzel beláttuk, hogy az

A B C

alapidom valóban szabályos háromszög.
Be fogjuk látni, hogy ez a feltétel elegendő is a megfelelő gömbhármas létezéséhez. Eközben egyszersmind meg is szerkesztjük a gömbközéppontokat:
Legyen a gúla beírt gömbjének középpontja

O

. Ez mind a 4 lapsíktól egyenlő távolságra van, az

O A

O B

O C

egyenes pontjai pedig rendre attól a 3‐3 lapsíktól vannak egyenlő távolságra, amelyek

A

-ban,

B

-ben, ill.

C

-ben futnak össze. Ezek az

A

, ill.

B

, ill.

C

csúcsú (és a gúlát tartalmazó) ún. triéder belső lapszögfelező síkjainak közös egyenesei. Eszerint

Q_{i}

rendre

O A

-n,

O B

-n, ill.

O C

-n van, és a

Q_{i}

, valamint

E_{i}

pontokkal meghatározott

K

háromoldalú szabályos hasáb úgy van beleírva az

O A B C

gúlába, hogy

E_{i}

csúcsai ennek

A B C

alapsíkján vannak,

Q_{i}

csúcsai pedig az

O

-ban összefutó oldaléleken.
Ennek a hasábnak a (fedőlapján levő)

Q_{i}

csúcsait egy csapásra megkaphatjuk egy

O

centrumú hasonlósági transzformáció útján. Megszerkesztjük az

A B C

lapra kifelé (szemléletesen mondva lefelé, alája) azt a

K'

egyenes hasábot, melynek

m

oldaléle fele akkora, mint az

A B C

háromszög oldalainak közös hossza,

K'

tehát hasonló a keresett

K

-hoz. Legyen az

A

B

C

-ből lefelé kiinduló oldalél végpontja rendre

H_{i}

‐ az általuk meghatározott háromszög szabályos, síkja párhuzamos

S_{D}

-vel. A

K'

lapjai páronként párhuzamosak a keresett

K

lapsíkjaival, továbbá fedőlapjaik csúcsai olyan párokba kapcsolhatók, melyek összekötő egyenesei átmennek

O

-n. Ezért mondhattuk előre, hogy

O

centrumú hasonlósági transzformációt használunk. Így az

O H_{i}

egyenesnek

S_{D}

-vel való metszéspontja a keresett

E_{i}

-t adja, az

E_{i}

-n át

S_{D}

-re állított merőleges egyenes pedig éppen

Q_{i}

-t metszi ki az

O A

O B

, ill.

O C

szakaszból.
Ugyanis ekkor

E_{i} Q_{i}

párhuzamos a hasáb

H_{i}

-n átmenő oldalélével, amit

S_{D}

-re merőlegesen szerkesztettünk, és pl.

E_{1} Q_{1}

benne van az

O A H_{1}

síkban.
Így a

H_{1} H_{2} H_{3}

háromszöget, az

E_{1} E_{2} E_{3}

háromszögbe átvivő hasonlósági transzformáció a

Q_{1} Q_{2} Q_{3}

háromszögbe viszi át az

A B C

háromszöget, tehát

K'

-t a

K

-ba. Eszerint

Q_{1} Q_{2} Q_{3}

háromszög szabályos, és,

Q_{1} Q_{2} : Q_{1} E_{1} = A B :

: A H_{1} = 2 : 1

.
Ha tehát

Q_{i}

körül

Q_{i} E_{i}

sugárral

G_{i}

gömböket írunk (

i = 1, 2, 3

), ezek páronként érintik egymást, és mindegyik érinti

S_{D}

-t. És ha vesszük

S_{D}

-nek az

A Q_{1} Q_{2}

síkra való tükörképét, ez egyfelől érinti

G_{1}

-et és

G_{2}

-t, másfelől azonos lesz

S_{C}

-vel, mert a tükrözés síkja tartalmazza

O

-t. Gömbjeink eszerint valóban teljesítik a követelményeket.

2. Ami a

Q_{i}

pontok megszerkesztését illeti ‐ adottnak tekintve a szabályos háromszög alapú

A B C D

gúlát ‐, elvi kérdés, mit értsünk szerkesztésen a térben, amikor a szokásos szerkesztéseinknek ‐ kimondatlanul ‐ állandó hordozója egy sík papírlap. Megoldóink ösztönösen helyesen dolgoztak, itt viszont ki is mondjuk az elveket:

Bármely adott (vagy korábbi lépés útján meghatározott) síkban szerkeszthetünk a síkbeli szabályok szerint.
Adott (meghatározott) a sík 3 ismert pontjával, hacsak ezek nincsenek egy egyenesben; egyértelmű ezzel a következő 3 változat: egyenes és rajta kívül fekvő pont, metsző egyenespár, párhuzamos egyenespár.
Ha adott egy sík és egy egyenes (amelynek van a síkon kívül levő pontja is), akkor adottnak tekintjük a közös pontjukat is.
Nem részletezzük, hogyan vezethető vissza ezekre merőleges sík és egyenes, ill. párhozamos sík és egyenes szerkesztése adott egyeneshez vagy síkhoz, valamint síkok metszésvonalának szerkesztése.

3. Ebben az értelemben csak a gúla

O

pontjának szerkesztését részletezzük, ami tulajdonképpen csak lapszög felezését jelenti. Az

A B

élű lapszög szárlapjaiból,

S_{D}

-ből és

S_{C}

-ből kimetsszük egy‐egy egyenesüket, az

A B

-n választott

X

ponton átmenő és

A B

-re merőleges sík révén. A két egyenes szögét felező egyenes

A B

-vel együtt meghatározza a szögfelező síkot.

Megjegyzés. A kitűző 1963-ban szerkesztette javaslatát. Hozzátette, hogy az 1962. évi Arany‐verseny egyik feladatát vitte át térre: Adott egy háromszög. Szerkesszünk két egyenlő sugarú kört úgy, hogy mind a két kör érintse a háromszög két oldalát és ezen kívül egymást is érintsék. (A megoldást lásd KöMaL 25. (1962) 104. oldal.)