Kezdőlap


Feladat:	F.2407	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Kós Géza
Füzet:	1983/október, 58 - 59. oldal		PDF \| MathML
Témakör(ök):	Terület, felszín, Szabályos sokszögek geometriája, Feladat, Síkgeometriai bizonyítások
Hivatkozás(ok):	Feladatok: 1983/február: F.2407

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A feladat állítása egyenértékű azzal, hogy a $B_{1} B_{2} ... B_{n}$ , $C_{1} C_{2}$ $... C_{n}$ sokszögeket az $A_{1} A_{2} ... A_{n}$ sokszöggé kiegészítő $B_{1} A_{2} B_{2}$ , $B_{2} A_{3} B_{3}$ , $...$ , $B_{n} A_{1} B_{1}$ ; illetve $C_{1} A_{2} C_{2}$ , $C_{2} A_{3} C_{3}$ , $...$ , $C_{n} A_{1} C_{1}$ háromszögek területének összege egyenlő.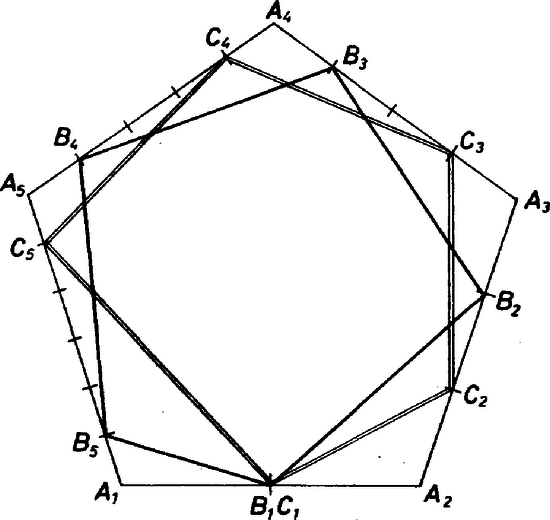

Legyen az

A_{1} A_{2} ... A_{n}

konvex szabályos sokszög szöge

α

, és oldala egységnyi. Ekkor a feladat szerint

i = 1, 2, ..., n - 1

esetében

\begin{matrix} B_{i} A_{i + 1} = \frac{1}{i + 1}, A_{i + 1} B_{i + 1} = (i + 1) \cdot \frac{1}{i + 2}, C_{i} A_{i + 1} = \frac{i}{i + 2}, A_{i + 1} C_{i + 1} = \frac{1}{i + 2} . \end{matrix}

B_{i} A_{i + 1} B_{i + 1}

, ill. a

C_{i} A_{i + 1} C_{i + 1}

háromszög területe:

\begin{matrix} T (B_{i} A_{i + 1} B_{i + 1}) = \frac{1}{2} B_{i} A_{i + 1} \cdot A_{i + 1} B_{i + 1} \cdot sin α = \frac{sin α}{2} \cdot \frac{i + 1}{(i + 1) (i + 2)}, \\ T (C_{i} A_{i + 1} C_{i + 1}) = \frac{1}{2} C_{i} A_{i + 1} \cdot A_{i + 1} C_{i + 1} \cdot sin α = \frac{sin α}{2} \cdot \frac{i}{(i + 1) (i + 2)} . \end{matrix}

i = n

esetén pedig hasonlóan

\begin{matrix} B_{n} A_{n + 1} = B_{n} A_{1} = \frac{1}{n + 1}, A_{1} B_{1} = A_{1} C_{1} = \frac{1}{2} és C_{n} A_{n + 1} = \frac{n}{n + 1} \end{matrix}

alapján

\begin{matrix} T (B_{n} A_{1} B_{1}) = \frac{sin α}{2} \cdot \frac{1}{2 (n + 1)}, T (C_{n} A_{1} C_{1}) = \frac{sin α}{2} \cdot \frac{n}{2 (n + 1)} . \end{matrix}

Így a következőt kell bizonyítanunk:

\begin{matrix} \sum_{i = 1}^{n - 1} \frac{i + 1}{(i + 1) (i + 2)} + \frac{1}{2 (n + 1)} = \sum_{i = 1}^{n - 1} \frac{i}{(i + 1) (i + 2)} + \frac{n}{2 (n + 1)} . \end{matrix}

A bal és a jobb oldal különbsége:

\begin{matrix} \sum_{i = 1}^{n - 1} \frac{1}{(i + 1) (i + 2)} + \frac{1 - n}{2 (n + 1)} = \sum_{i = 1}^{n - 1} (\frac{1}{i + 1} - \frac{1}{i + 2}) + \frac{1 - n}{2 (n + 1)} = \frac{1}{2} - \frac{1}{n + 1} + \frac{1 - n}{2 (n + 1)} . \end{matrix}

Ez pedig 0. Ezzel az állítást igazoltuk.

Kós Géza (Budapest, Berzsenyi D. Gimn., I. o. t.)