Feladat: F.2403 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Alexy N. ,  Ambrus L. ,  Balga A. ,  Balog 444 P. ,  Beke S. ,  Bujdosó 419 L. ,  Böröczky L. ,  Csillag P. ,  Danyi P. ,  Erdős 228 L. ,  Fáth G. ,  Fülöp T. ,  Gulyás Éva ,  Hajós Zsuzsanna ,  Hegedűs Andrea ,  Herendi T. ,  Hetyei G. ,  Horváth 290 P. ,  Horváth B. ,  Hraskó A. ,  Ispány Márton ,  Kántor Cs. ,  Kapovits Á. ,  Katona Gy. ,  Kerner Anna ,  Kis 117 A. ,  Kovács 829 T. ,  Kovács I. 111 S. ,  Kovalcsik I. ,  Ladányi L. ,  Lengyel Zs. ,  Megyesi G. ,  Mócsy M. ,  Nyikes P. ,  Pásztor L. ,  Peták T. ,  Scharle A. ,  Simon P. ,  Szabó 112 T. ,  Szabó 741 Z. ,  Szederkényi Edit ,  Szekeres G. ,  Szöllősi Gabriella ,  Tóth G. ,  Törőcsik J. ,  Varga K. ,  Virányi L. ,  Vityi P. 
Füzet: 1983/november, 121 - 122. oldal  PDF  |  MathML 
Témakör(ök): Egyenesek egyenlete, Mértani helyek, Terület, felszín, Feladat
Hivatkozás(ok):Feladatok: 1983/január: F.2403

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a rombusznak az AB, BC, CD oldalszakaszon levő csúcsát rendre P, Q, R betűvel, és legyen még E, F a négyzet BC, AD oldalának felezőpontja. A rombusz K középpontja ‐ mint a PR szakasz felezőpontja az EF szakaszra esik, a kérdéses S negyedik csúcs pedig Q-nak K-ra vonatkozó tükörképe. Következésképp S pontja lesz a BC'B'C téglalapnak, ahol B'C' a BC oldalnak F-re vonatkozó tükörképe; de S nem pontja a BC szakasznak.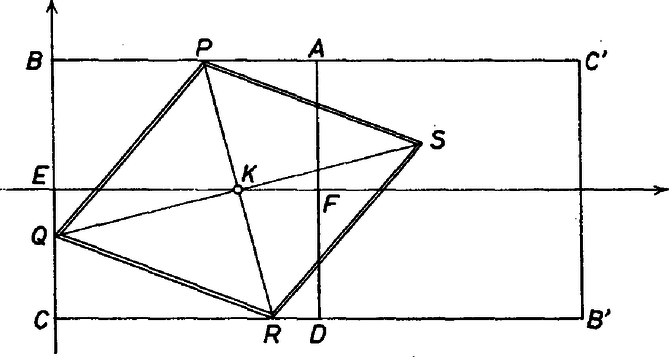

 
 

1. ábra
 

 

Az S pontok által befutott halmazt abban a koordináta‐rendszerben írjuk le, amelynek origója E, továbbá F az (1; 0) pont, ennélfogva B koordinátái (0, 1/2). Legyen még S(x,y) a BC'B'C téglalap egy pontja, vagyis teljesüljenek az
0<x≤2,-1/2≤y≤1/2(1)
egyenlőtlenségek. Nézzük meg, milyen további feltételeket kell tennünk x-re és y-ra, hogy S egy megfelelő rombusz negyedik csúcsa lehessen.
Mivel K felezi a QS szakaszt, továbbá rajta van az EF egyenesen, azért Q és K koordinátái szükségképpen
K(x/2,0),Q(0,-y).
Az (1) föltevés miatt így Q a BC szakasz pontja lesz. A rombusz P és R csúcsát a K-ban QS-ra állított merőleges egyenes metszi ki az AB, illetve CD egyenesből, a metszéspontok koordinátái
P(x2-yx,12),R(x2+yx,-12).
Ha S egy megfelelő rombusz negyedik csúcsa, annak további csúcsai csak a most kapott P, Q, R pontok lehetnek. Ezért S(x,y) akkor és csak akkor tartozik hozzá a keresett idomhoz, ha (1) mellett még a
0≤x2-yx≤1,0≤x2+yx≤1(2)
föltételek is teljesülnek. Így feladatunk az, hogy meghatározzuk annak az idomnak a területét, melyet az (1) és (2) feltételt kielégítő, (x,y) koordinátájú pontok alkotnak.
A (2) egyenlőtlenségeket az (1) szerint pozitív x-szel végigszorozva, majd átrendezve
-x2≤2y≤x2,-1+(1-x)2≤2y≤1-(1-x)2.(3)
A (3) egyenlőtlenségek által definiált idomot láthatjuk a 2. ábrán.
 
 

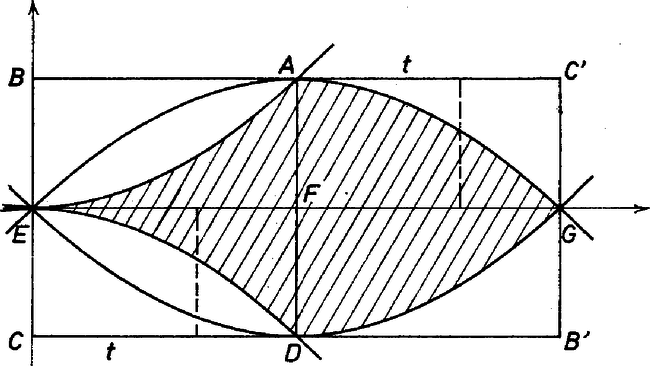2. ábra
 

 

A görbe vonalak egybevágó parabolaívek. Mivel ez része a BC'B'C téglalapnak, azért ennek és csak ennek a pontjai teljesítik (1)-et és (2)-t is. Következésképp ennek az idomnak a területét kell meghatároznunk.
(3)-ból leolvasható, hogy az idomnak az AC'GF téglalapba eső része egybevágó az EFDC téglalapból hiányzó résszel. Valóban, húzzuk meg az AC'GF téglalapban az AF-fel párhuzamos, AF-től t távolságra levő, 1/2 hosszúságú szakaszt. Idomunk ezt a szakaszt két részre vágja: az alsó
12(1-[1-(1+t)]2)=12(1-t2)
hosszúságú része az idomhoz tartozik, a felső, t2/2 hosszúságú rész már nem. Hasonlóan elvágva az EFDC téglalapot, itt a felső t2/2 hosszúságú rész tartozik az idomhoz, az alsó, (1-t2)/2 hosszúságú rész nem. Következésképp a kérdéses idomnak a két téglalapban található része éppen akkora területű, mint az EFDC téglalap.
Hasonlóan igazolható, hogy az FGB'D és BAFE téglalapokba eső részek együttesen akkora területűek, mint a BAFE téglalap. A keresett idom területe tehát megegyezik az ABCD négyzet területével.