Kezdőlap


Feladat:	F.2378	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Danyi Pál , Megyesi Gábor
Füzet:	1983/március, 109 - 112. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Egyenlő szárú háromszögek geometriája, Beírt kör, Terület, felszín, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1982/szeptember: F.2378

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen az $A B C$ szabályos háromszög $B C$ , $C A$ , $A B$ oldalának felezőpontja, más szóval a beírt kör érintési pontja rendre $D$ , $E$ , $F$ . Legyen $P$ egyelőre ezektől különböző pontja a beírt körnek, és $P$ -nek szóban forgó vetületei rendre $A_{1}$ , $B_{1}$ , $C_{1}$ , végül a $D E F$ középháromszög $E F$ , $F D$ és $D E$ oldalegyenesén levő vetülete rendre 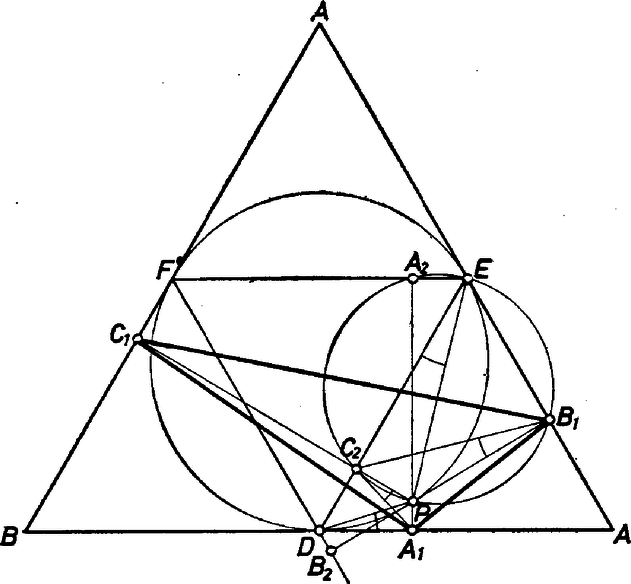$A_{2}$ , $B_{2}$ , $C_{2}$ .

A merőleges szárú szögek tétele szerint a

P A_{1}

P B_{1}

P C_{1}

félegyenesek páronként

120^{\circ}

-os szöget zárnak be egymással. Ezért

P

mindig benne van a kérdéses

A_{1} B_{1} C_{1}

háromszögben, tehát ennek területét a

P A_{1} B_{1}

P B_{1} C_{1}

P C_{1} A_{1}

háromszögek területének összegeként kapjuk. Közös tényezőjüket kiemelve

\begin{matrix} t = \frac{sin 120^{\circ}}{2} (P A_{1} \cdot {P B}_{1} + P B_{1} \cdot {P C}_{1} + P C_{1} \cdot {P A}_{1}) . \end{matrix}

Elég tehát megmutatnunk, hogy a zárójelbeli

K

kifejezés állandó.
Belátjuk, hogy

P A_{1} \cdot {P B}_{1} = P C_{2}^{2}

. A vetítések folytán

A_{1}

és

C_{2}

rajta vannak a

P D

szakasz fölötti Thalész-körön,

B_{1}

és

C_{2}

pedig a

P E

szakasz fölötti Thalész-körön. A kerületi szögek tétele alapján ábránk szerint

\begin{matrix} P B_{1} C_{2} ∢ = P E C_{2} ∢ = P E D ∢ = P D A_{1} ∢ = P C_{2} A_{1} ∢ . \end{matrix}

Felhasználtuk, hogy felvételünkben

C_{2}

D E

szakasz belső pontja, másrészt hogy a

P E D

és

P D A_{1}

szögek a beírt körre nézve is kerületi szögek.
Így a

P B_{1} C_{2}

és

P C_{2} A_{1}

háromszögek

2 - 2

szöge egyenlő, tehát hasonlók és csúcsaik a felírás sorrendjében felelnek meg egymásnak. Ebből

\begin{matrix} P B_{1} : P C_{2} & = P C_{2} : P A_{1}, \\ P A_{1} \cdot {P B}_{1} & = P C_{2}^{2}, \end{matrix}

amint állítottuk.
Tovább alakítjuk az összefüggést. Ábránkat és a szabályos háromszög összefüggéseit felhasználva

\begin{matrix} P A_{1} \cdot {P B}_{1} = {(P C_{1} - C_{2} C_{1})}^{2} = {(P C_{1} - \frac{C F}{2})}^{2} = {(P C_{1} - \frac{\sqrt[]{3}}{4} A B)}^{2} = \\ = P C_{1}^{2} - \sqrt[]{3} \frac{A B \cdot {P C}_{1}}{2} + \frac{3}{16} A B^{2} . \end{matrix}

Lényegében ugyanígy kapjuk az alábbiakat:

\begin{matrix} P B_{1} \cdot {P C}_{1} = P A_{1}^{2} - \sqrt[]{3} \frac{B C \cdot {P A}_{1}}{2} + \frac{3}{16} A B^{2}, \\ P C_{1} \cdot {P A}_{1} = P B_{1}^{2} - \sqrt[]{3} \frac{C A \cdot {P B}_{1}}{2} + \frac{3}{16} A B^{2} . \end{matrix}

(A gondolatmenetben átmenetileg két kis módosulás van, de azok a végeredményt nem érintik:

B_{2}

D F

oldal meghosszabbításán keletkezik, továbbá

P

belső pontja az

A_{1} A_{2}

B_{1} B_{2}

szakaszoknak.)
Ezek összeadásával

\begin{matrix} K = (P A_{1}^{2} + P B_{1}^{2} + P C_{1}^{2}) - \sqrt[]{3} \cdot \frac{1}{2} (A B \cdot {P C}_{1} + B C \cdot {P A}_{1} + C A \cdot {P B}_{1}) + \frac{9}{16} A B^{2} . \end{matrix}

Felismerjük a második tagban az

A B C

háromszög területét mint a

P A B

P B C

P C A

részháromszögek területének összegét,

\sqrt[]{3}

-mal szorozva. Ez a részlet tehát

- \frac{3}{4} A B^{2}

. Az innen adódó

\begin{matrix} P A_{1} + P B_{1} + P C_{1} = \frac{\sqrt[]{3}}{2} A B \end{matrix}

kifejezést ‐ ami egyébként a szabályos háromszög minden belső pontjára érvényes ‐, a távolságok négyzetösszegének átalakítására is felhasználjuk, és ezáltal egyenletet kapunk a

K

kifejezésre.

K

definíciója alapján

\begin{matrix} P A_{1}^{2} + P B_{1}^{2} + P C_{1}^{2} = {(P A_{1} + P B_{1} + P C_{1})}^{2} - 2 K, \\ K = - 2 K + \frac{9}{16} A B^{2}, \end{matrix}

és máris látjuk, hogy

K

állandó. Ezzel bebizonyítottuk az állítás.
Felírjuk az

A_{1} B_{1} C_{1}

háromszög területének explicit kifejezését is, az

A B C

háromszög

T

területével:

\begin{matrix} t = \frac{\sqrt[]{3}}{4} K = \frac{\sqrt[]{3}}{4} \cdot \frac{3}{16} A B^{2} = \frac{3}{16} T . \end{matrix}

Ez az eredmény közvetlenül is adódik a speciális esetekben, ti. ha

P

-t

D

-ben vagy a

C F

szimmetriatengelyen választjuk. Az

A_{1} B_{1} C_{1}

egyenlő szárú háromszög alapja és magassága az első esetben

\frac{3}{4} A B

, ill.

\frac{1}{4} A D

, a másodikban

\frac{1}{4} A B

, ill.

\frac{3}{4} C F

Danyi Pál (Pécs, Nagy Lajos Gimn., IV. o. t.)

II. megoldás. Tovább használjuk az I. megoldás jelöléseit, legyen továbbá a beírt kör középpontja

O

, a körnek az

O C

félegyenesen levő pontja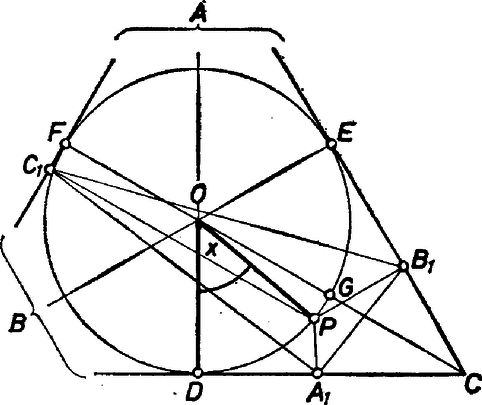

G

A szimmetria alapján elég az állítást a kör rövidebbik

D G

ívére bizonyítani. Legyen

P

ennek pontja, továbbá

O D = ϱ = 1

és

D O P ∢ = x

. Ekkor

\begin{matrix} P A_{1} & = 1 - cos x, \\ P B_{1} & = 1 - cos (x - 120^{\circ}), \\ P C_{1} & = 1 - cos (x - 240^{\circ}), \end{matrix}

ezekkel az I. megoldás

K

kifejezése így alakul:

\begin{matrix} 3 & - 2 (cos x + cos (x - 120^{\circ}) + cos (x - 240^{\circ})) + \\ + cos x (cos (x - 120^{\circ}) + cos (x - 240^{\circ})) + \\ + cos (x - 120^{\circ}) cos (x - 240^{\circ}) . \end{matrix}

2

-vel szorzott zárójel értéke az addíciós tétel alkalmazásával

0

. A következő zárójelben

- cos x

áll, az utolsó szorzat pedig a

2 cos u cos v = cos (u - v) + cos (u + v)

azonosság alkalmazásával

\begin{matrix} \frac{1}{2} (cos 120^{\circ} + cos 2 x) = \frac{1}{2} (- \frac{1}{2} + 2 cos^{2} x - 1) = - \frac{3}{4} + cos^{2} x . \end{matrix}

Ezek szerint a

K

kifejezés

x

-et tartalmazó tagjainak összege

0

, a terület nem függ

x

-től. Az állítást bebizonyítottuk.
Az

A_{1} B_{1} C_{1}

háromszög területe számításunk szerint

\frac{sin 120^{\circ}}{2} \cdot \frac{9}{4} = \frac{9 \sqrt[]{3}}{16} (\approx 0,974 egység)

. Másrészt az

A B C

háromszög magassága

3

, oldala

2 \sqrt[]{3}

, területe

3 \sqrt[]{3}

, a két terület aránya

\frac{3}{16}

Megyesi Gábor (Szeged, Ságvári E. Gyak. Gimn., II. o. t.)

Megjegyzés. A feladat kapcsolatban áll az 1977. évi OKTV. II. fordulójának két feladatával is, amelyek az I., ill. II. szakosítású matematikai osztályok versenyzői részére voltak kitűzve. (Lásd a Középiskolai Matematikai Versenyek 1977 - 1979. c. gyűjtemény, Tankönyvkiadó, Bp., 1981. 106., ill. 109. feladatát és a hozzá kapcsolódó megjegyzéseket.)