Kezdőlap


Feladat:	F.2371	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1982/december, 202 - 204. oldal		PDF \| MathML
Témakör(ök):	Egyéb sokszögek geometriája, Feladat, Síkgeometriai bizonyítások, Középponti és kerületi szögek
Hivatkozás(ok):	Feladatok: 1982/május: F.2371

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a $C_{1} C_{4}$ , $C_{2} C_{5}$ és $C_{3} C_{6}$ szakasz felezőpontját rendre $F_{1}, F_{2}, F_{3}$ betűvel, a $C_{1} C_{4}, C_{2} C_{5}$ , és $C_{3} C_{6}$ egyenesek közös pontját pedig ‐ mint már a 2365. feladatban ‐ $P$ -vel. Az állítást az ábráinkon látható felvételek esetére azzal bizonyítjuk, hogy az $F_{1} F_{3}$ szakasznak $P$ -ből vett látószöge egyenlő az $F_{2}$ -ből vett látószögével. Más felvételen előfordulhat, hogy $P$ és $F_{2}$ az $F_{1} F_{3}$ egyenes két különböző partján van, ilyenkor a két látószög $180^{\circ}$ -ra egészíti ki egymást, ami lényegében ugyanúgy bizonyítható.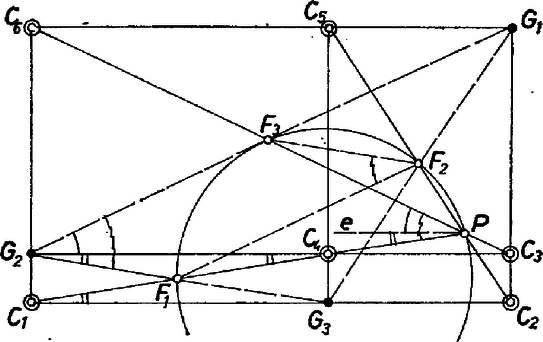
Természetesen külön tárgyaljuk majd a hatszög olyan helyzeteit, amelyekben $P$ nem jön létre. Látni fogjuk, hogy ilyenkor a felezőpontok egy egyenesre esnek, tehát ugyanekkor a szóban forgó kör sem jön létre, illetve elfajul ,,végtelen sugarúvá".

1. ábra

1. A bizonyításba bevonjuk azt a három pontot is, amelyet hatszögünk szemben levő oldalegyenes párjai határoznak meg, legyen a

C_{2} C_{3}

C_{5} C_{6}

oldalpár metszéspontja

G_{1}

, a

C_{3} C_{4}, C_{6} C_{1}

, páré

G_{2}

, a

C_{4} C_{5}, C_{1} C_{2}

páré

G_{3}

. (Más szóval a közös irányú 3‐3 oldalegyenes által meghatározott mind a 9 pontnak szerepe van az alakzatban.) Azt a 3 téglalapot használjuk fel, amelyeknek a csúcsai váltakozva

C

és

G

típusú pontok. Egyik ilyen a

C_{1} G_{2} C_{4} G_{3}

, ebben a kérdéses

F_{1}

pont a

G_{2} G_{3}

átlót is felezi. Ugyanígy felezi

F_{2}

G_{3} G_{1}

szakaszt,

F_{3}

G_{1} G_{2}

-t, ennélfogva az

F_{1} F_{2} F_{3}

háromszög a

G_{1} G_{2} G_{3}

háromszög középháromszöge, tehát szögeik páronként rendre egyenlők.
Vegyük a

P

-n átmenő és

C_{1} C_{2}

-vel párhuzamos

e

félegyenest. Ezzel az

F_{1} P F_{3}

látószöget két részre osztjuk (1. ábra), ill.

e

ugyanazon oldalán fekvő két szög különbségeként állíthatjuk elő (2. ábra). A részek rendre egyenlők az említett téglalapokban az

e

-vel párhuzamos oldal és az átló közti szöggel:

\begin{matrix} F_{3} P e ∢ = F_{3} C_{3} G_{2} ∢ = F_{3} G_{2} C_{3} ∢, \\ F_{1} P e ∢ = F_{1} C_{4} G_{2} ∢ = F_{1} G_{2} C_{3} ∢, \end{matrix}

ennélfogva mindkét felvétel esetében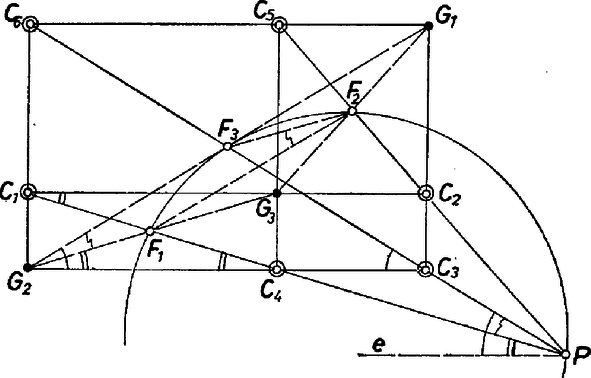

\begin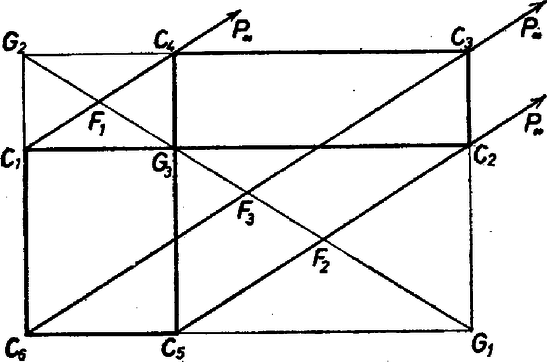{matrix} F_{3} P F_{1} ∢ = F_{3} G_{2} F_{1} ∢ \pm F_{1} G_{2} C_{3} ∢ = F_{3} G_{2} F_{1} ∢ = F_{3} F_{2} F_{1} ∢, \end{matrix}

ezt akartuk bizonyítani, és ezzel azt is bebizonyítottuk, amit kellett.

2. ábra

2. Ha

P

nem jön létre, ez azt jelenti, hogy a felhasznált téglalapok hasonlóak, (mert egyeznek az átlóknak az oldalakkal alkotott szögei.) Így

F_{1} G_{2} C_{3} ∢ = F_{3} G_{2} C_{3} ∢ = F_{3} G_{3} C_{2} ∢

F_{2} G_{3} C_{2} ∢

, a

G_{1} G_{2} G_{3}

és

F_{1} F_{2} F_{3}

háromszögeket meghatározó pontok egy egyenesbe esnek (3. ábra).

3. ábra

Ez a 2365. feladat I. megoldása (4) összefüggésének megfelelője.

Megjegyzések. 1. Visszatekintve a 2365. feladatra, látjuk, hogy itt fel kellett használnunk a merőlegességet a 3‐3 oldalegyenes között ‐ a téglalapok szögeinek egyenlőségében. Eszerint a feladat állítása ferdén hajló egyeneshármasok esetében nem érvényes.
2. Egy dolgozat azzal az ellenpéldával vélte bizonyítani a feladat állításának ,,valótlanságát", amely a 3. ábrából jön létre, amikor bármelyik két szomszédos párhuzamos között ugyanakkora a távolság. A beküldő ‐ sajnos ‐ még eléggé távol áll a matematikai gondolkodástól. Nem azt akarjuk ezzel mondani, hogy nem szabad megnézni különlegesen egyszerű helyzeteket, hanem azt, hogy nem szabad ezek után megállni. Keresni kell, hogy mi igaz a kitűzésből a szó legszorosabb értelmében, továbbá hogy mit jelentenek az elfajulások.
3. Ha rögzítjük az

F

ponthármast, vagyis a

G

-hármast is, a kör változatlan marad. A kör bármely pontját

P

-nek választva, megkapható az őt előállító

C

-ponthatos: a

P F

szelők metszik ki őket párosával a

G_{i} G_{j}

átmérőjű körökből.