Kezdőlap


Feladat:	F.2365	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1982/december, 199 - 202. oldal		PDF \| MathML
Témakör(ök):	Egyenesek egyenlete, Egyéb sokszögek geometriája, Feladat, Síkgeometriai bizonyítások
Hivatkozás(ok):	Feladatok: 1982/április: F.2365

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Válasszuk koordináta-rendszerünk origójául a $C_{1}$ csúcsot, $x$ tengelyéül a $C_{1} C_{2}$ egyenest, legyen $C_{2}$ abszcisszája $a_{2}$ és $C_{3}$ ordinátája $b_{3}$ . Ekkor a feladat szerint az $y$ tengely a $C_{1} C_{6}$ egyenes lesz, jelöljük $C_{6}$ ordinátáját $b_{6}$ -tal és $C_{5}$ abszcisszáját $a_{5}$ -tel. Így a hatszög csúcsai:

\begin{matrix} C_{1} (0 : 0), C_{2} (a_{2}, 0), C_{3} (a_{2}, b_{3}), C_{4} (a_{5}, b_{3}), C_{5} (a_{5}, b_{6}) és C_{6} (0, b_{6}), \end{matrix}

és azt kell belátnunk, hogy a

C_{2} C_{5}

és

C_{6} C_{3}

egyenesek

P

metszéspontja rajta van a

C_{1} C_{4}

egyenesen, melynek egyenlete

\begin{matrix} y = \frac{b_{3}}{a_{5}} x . \end{matrix}

Természetesen

a_{2}

és

a_{5}

különbözők egymástól és

0

-tól, hasonlóan

b_{3}

és

b_{6}

is egymástól és

0

-tól.
A mondott egyenesek egyenlete rendre

\begin{matrix} y = \frac{b_{6}}{a_{5} - a_{2}} (x - a_{2}), ill. y = b_{6} + \frac{b_{3} - b_{6}}{a_{2}} x, \end{matrix}

(1)

ezekből

P

abszcisszája

\begin{matrix} x_{P} = \frac{a_{2} a_{5} b_{6}}{a_{2} b_{6} - (a_{5} - a_{2}) (b_{3} - b_{6})}, \end{matrix}

(2)

hacsak a

N

nevező nem tűnik el, azaz ha

\begin{matrix} N = a_{2} b_{6} - (a_{5} - a_{2}) (b_{3} - b_{6}) = a_{2} (a_{5} - a_{2}) (\frac{b_{6}}{a_{5} - a_{2}} - \frac{b_{3} - b_{6}}{a_{2}}) \neq 0, \end{matrix}

vagyis ha (1)-ben az iránytangensek különbözők. Ekkor

P

ordinátájára a második egyenletből

\begin{matrix} \frac{y_{P}}{b_{6}} = 1 + \frac{(b_{3} - b_{6}) a_{5}}{N} = \frac{a_{2} b_{3}}{N} . \end{matrix}

(3)

Mármost (3) és (2) egybevetéséből valóban

\begin{matrix} \frac{y_{P}}{x_{P}} = \frac{b_{3}}{a_{5}}, \end{matrix}

ezt akartuk bizonyítani.
Ha azonban az (1)-beli iránytényezők egyenlők, vagyis

C_{2} C_{5} ∥ C_{6} C_{3}

, ebből átalakítással

\begin{matrix} \frac{b_{6}}{b_{3} - b_{6}} = \frac{a_{5} - a_{2}}{a_{2}} \end{matrix}

(4)

(egyik nevező sem nulla !), mindkét oldalhoz 1-et adva

\begin{matrix} \frac{b_{3}}{b_{3} - b_{6}} = \frac{a_{5}}{a_{2}}, és így \frac{b_{3}}{a_{5}} = \frac{b_{3} - b_{6}}{a_{2}}, \end{matrix}

azaz

C_{1} C_{4} ∥ C_{6} C_{3}

. Ilyenkor a kérdéses három egyenes közül semelyik kettő nem metszi egymást, és a feladat állítása ,,projektív értelemben'' igaz, vagyis ahogyan azt szokás mondani, hogy párhuzamos egyeneseknek a végtelen távolban van a közös pontja, és hogy a különböző irányokhoz tartozó végtelen távoli pontok a végtelen távoli egyenest alkotják.

Megjegyzés. A párhuzamosság esetére talált (4) feltétel a 3‐3 párhuzamos oldalegyenes közti távolságok között összefüggést jelent, hiszen pl.

| b_{3} - b_{6} |

C_{3} C_{4}

és

C_{5} C_{6}

egyenesek távolsága.

II. megoldás. Elemi meggondolásokkal is célhoz érhetünk. Elég tulajdonképpen egyetlen tájékoztató ábra is, ha abból a föltevésnek csak a következő tartalmát olvassuk ki:

α)

k = 1, 2, 3

esetén a

C_{2 k} C_{2 k - 1}

egyenesek

i'

iránya közös, másrészt a

C_{2 k} C_{2 k + 1}

egyenesek

i''

iránya is ‐ ahol

C_{7}

-en is a

C_{1}

csúcsot értjük;

β)

a 3‐3 párhuzamos egyenes különböző.
Azt azonban egyik hármasban sem akarjuk felhasználni, hogy melyik egyenes van a másik kettő között. Nem használjuk ki azt sem, hogy

i''

merőleges

i'

-re, csupán azt, hogy

i'

és

i''

különböző irányok.

1. Tegyük föl, hogy a

C_{2} C_{5}

és

C_{3} C_{6}

egyeneseknek van közös

P

pontjuk, és jelöljük

P C_{1}

és

C_{3} C_{4}

metszéspontját

M

-mel (1. ábr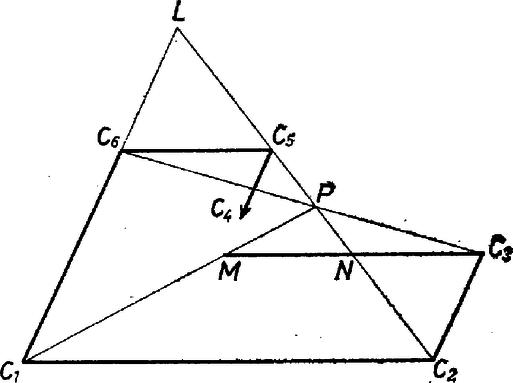a).

1. ábra

(Könnyű belátni, hogy

P

nem lehet rajta egyiken sem a 3‐3 oldalegyenes közül.) Azt mutatjuk meg, hogy

C_{5} M ∥ C_{6} C_{1}

. Ebből már következik, hogy

M

azonos

C_{4}

-gyel, tehát

P

-n az állításbeli

C_{1} C_{4}

egyenes is átmegy.
Jelöljük a

C_{2} C_{5}

egyenesnek

C_{1} C_{6}

-on levő metszéspontját

L

-lel,

C_{3} C_{4}

-en levő pontját

N

-nel. Ezáltal a

C_{5} C_{6}

és

N C_{3}

párhuzamos szakaszokra támaszkodva két pár hasonló háromszöget használhatunk fel, további oldalpárjaik párhuzamosak, ill. egy egyenesbe esnek.
Az

L C_{5} C_{6}

és

C_{2} N C_{3}

háromszög-pár megfelelő oldalaira teljesül

\begin{matrix} \frac{C_{5} C_{6}}{C_{5} L} = \frac{N C_{3}}{N C_{2}}, \end{matrix}

és a

P C_{5} C_{6}

P N C_{3}

párban

\begin{matrix} \frac{P C_{5}}{C_{5} C_{6}} = \frac{P N}{N C_{3}} . \end{matrix}

E két egyenlőséget összeszorozva a

C_{2} C_{5}

egyenesen keletkezett 4 szakasz között kapunk kapcsolatot:

\begin{matrix} \frac{P C_{5}}{C_{5} L} = \frac{P N}{N C_{2}} . \end{matrix}

A jobb oldal pedig egyenlő a

\frac{P M}{M C_{1}}

arány értékével, hiszen

C_{1} C_{2}

párhuzamos

M N

-nel, eredeti jelölése szerint

C_{3} C_{4}

-gyel. Most már a

\begin{matrix} \frac{P C_{5}}{C_{5} L} = \frac{P M}{M C_{1}} \end{matrix}

arány a párhuzamos szelők tételének megfordítása alapján azt jelenti, hogy

C_{5} M

párhuzamos

L C_{1}

-gyel, vagyis

C_{6} C_{1}

-gyel. Ezt akartuk belátni. ‐ Hozzátesszük még, hogy a feladat feltételei szerint

P

C_{2} L

szakaszhoz képest ugyanúgy helyezkedik el, mint a

C_{3} C_{6}

szakaszhoz képest ‐ vagyis vagy magán e két szakaszon van rajta, vagy a szakasz kezdőpontján inneni meghosszabbításon van, vagy pedig a végponton túli meghosszabbításon ‐, továbbá folytatólag ugyanúgy helyezkedik el

P

N C_{5}

-höz képest is, mint a

C_{3} C_{6}

-hoz. Másrészt

P

M C_{1}

-hez képest is ugyanúgy helyezkedik el, mint

N C_{2}

-höz képest, vagyis ahogyan a

C_{5} L

-hez képest. Más szóval azt jelentik ezek, hogy akkor is igazak számításaink, ha a távolságokhoz valami egységes elv szerint előjelet kapcsolunk, mintegy koordináta-rangra emeljük őket.
2. Ha

P

nem jön létre, vagyis

C_{2} C_{5} ∥ C_{3} C_{6}

, akkor megmutatjuk, hogy

C_{1} C_{4}

is párhuzamos velük. Ezt visszavezetjük az előzőkre. Ha

C_{1} C_{4}

metszené ‐ mondjuk ‐

C_{2} C_{5}

-öt egy

Q

pontban, akkor először jelölés- (ill. index-) cserét végzünk:

C_{i}

helyére

C_{i + 1}

-et írunk

i = 1, 2, 3, 4, 5

mellett, és

C_{6}

helyére

C_{1}

-et. Így a feltételezett

Q

pont az új

C_{2} C_{5}

és

C_{3} C_{6}

egyenesek metszéspontja, és a föntiek szerint átmegy rajta az új

C_{4} C_{1}

is, vagyis az eredeti

C_{6} C_{3}

. Föltevésünk második része ellentmondásra jut az első résszel, ez bizonyítja az ellentétes állítás lehetetlenségét.

Megjegyzések. 1. Több versenyző túl sok változatot vizsgált a hatszög csúcsainak kölcsönös helyzetére, mások viszont egyáltalán nem törődtek evvel. Lényegében csak kétféle ábratípus lehetséges: a 3‐3 párhuzamos közül a középsőknek a közös pontja vagy szerepel a 6 csúcs között, vagy pedig nem (2. ábra). Az indexelést fölösleges tekinteni, mert az állításban az indexelés szimmetrikus, amit az ellentmondásra vezető meggondolásban fel is használtunk, hangsúlyozása nélkül. Csak a második típusban lehetséges, hogy a

C_{1} C_{4}

C_{2} C_{5}

és

C_{3} C_{6}

egyenesek párhuzamosak legyenek.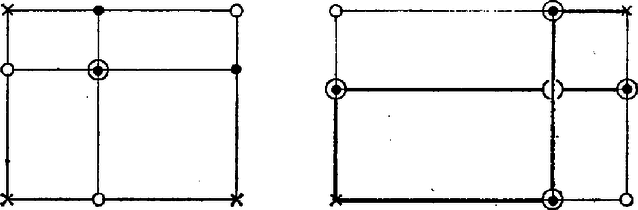

2. ábra

2. A II. megoldás mutatja, hogy tulajdonképpen nem is lehetett volna kihasználni az eredeti hatszög derékszögeit, csak a matematikai gondolkodás ,,arculcsapásával'', fölösleges elemként beleerőltetve a meggondolásba. Rámutatunk a feladat eredeti szövegére, az nem beszélt szögekről, csak merőleges állású oldalegyenes-párokról.
Az I. megoldásból amiatt nem adódhatott ki ez az észrevétel, mert az iskolai oktatásban még a derékszögű koordináta-rendszer használatára is csak kevés idő jut, szó sem eshet ferdeszögű koordináta-rendszerről.
Más szemszögből nézve ezt kaptuk: ha ábránkat párhuzamos vetítéssel átvisszük egy tetszőleges másik (vagyis az eredetivel nem párhuzamos) síkra, egyeneseink képe egyenes lesz, meglesz a közös pontjuk is, megmaradnak a párhuzamosságok is de a derékszögek általában nem maradnak meg.