Kezdőlap


Feladat:	F.2359	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Ákosfai Z. , Alberti G. , Almássy T. , Ambrosz O. , Ambrus L. , Balázs Z. , Bánhegyi B. , Bobák Emese , Borsó Zs. , Böröczky K. , Drávucz Katalin , Engländer J. , Erdős L. , Finta P. , Hetyei G. , Holbok I. , Jaklis S. , Kis A. , Lengyel L. , Magyar Á. , Megyesi G. , Mikó Teréz , Mohay T. , Molnár L. , Nádor P. , Nyikes P. , Peták T. , Somlói J. , Szabó Cs. , Szabó E. , Szöllősi Gabriella , Tóth G. , Tóth L. , Tranta Beáta , Törőcsik J. , Ván P. , Weisz F. , Zieger B.
Füzet:	1982/november, 125 - 127. oldal		PDF \| MathML
Témakör(ök):	Trapézok, Párhuzamos szelők tétele, Ellipszis, mint mértani hely, Feladat
Hivatkozás(ok):	Feladatok: 1982/március: F.2359

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A szöveg szerint a négyszög $C D$ oldala mozog, tehát a rögzített oldal $A B$ . És akkor $C D | | A B$ , továbbá a $C D$ oldal változatlan $c$ hossza kisebb $A B = a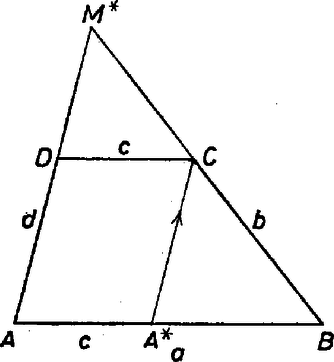$ -nál.

Jelöljük az

A D

és

B C

szárak metszéspontját

M

-mel, ez

c < a

, valamint a trapéz konvexsége alapján mindig létezik és az

A B

egyenesnek a

C D

-t tartalmazó partján van. Legyen még

A M = d

B M = b

, végül a változó oldalak állandó összege

A D + D C + C B = k

.
A párhuzamos szelők tétele alapján a szárak hossza:

\begin{matrix} A D = (1 - \frac{c}{a}) d, C B = (1 - \frac{c}{a}) b, \end{matrix}

ezeket a föltételi egyenlőségbe helyettesítve

\begin{matrix} (1 - \frac{c}{a}) (d + b) + c = k, \end{matrix}

és átrendezve az

M A

és

M B

távolságok összege

\begin{matrix} d + b = \frac{a}{a - c} (k - c) = \frac{k - c}{a - c} a = λ a . \end{matrix}

Itt a jobb oldal egyfelől állandó, másfelől a második alak szerint nagyobb, mint

a

, hiszen a trapéz létezik, tehát

k > a

; más szóval

λ > 1

. Eszerint

M

mindig rajta van azon az ellipszisen, amelynek fókuszai a rögzített

A

B

csúcsok és nagytengelyének hossza

λ a

.
Megfordítva,

M

ennek az ellipszisnek minden pontjába eljut ─ kivéve a nagytengelyének a végpontjait ─, mert az ellipszis minden ki nem zárt pontjához található

C D

-nek azt előállító helyzete. Legyen

M^{*}

az ellipszis tetszőleges, ki nem zárt pontja ‐ így

M^{*} A B

valóságos háromszög, továbbá

A^{*}

az a pontja az

A B

alapnak amelyre

A A^{*} = c (< a = A B)

. Az

A^{*}

-on átmenő és

M^{*} A

-val párhuzamos egyenes

M^{*} B

-t nyilván a megfelelő

C

pontban metszi.
Az ellipszis nagytengelyének végpontját véve

M

-nek, a trapéz elfajulna, hiszen

C

D

is rajta lenne

A B

-n, igy pedig

A D

és

B C

közös pontja határozatlan.

II. megoldás. Az előző megoldás ábrájához kapcsolódva

A^{*} C = A D

, ennélfogva

\begin{matrix} A^{*} C + C B = A C + D C + C B - D C = k - c, \end{matrix}

állandó,

C

rajta van azon az

e_{1}

ellipszisen, amelynek fókuszai

B

és

A^{*}

(utóbbi az adatokból egyértelműen meghatározható), és vezérsugarainak összege állandóan

(k - c)

.
Másrészt

M

B C

félegyenesen van, és ─ mint már felhasználtuk,

\begin{matrix} B M = b = \frac{a}{a - c} \cdot B C, \end{matrix}

ezért

M

pályája az

e_{1}

-nek

B

centrumú

a / (a - c)

arányú nagyított képe, ellipszis.
Másik

F_{2}

fókusza az

A^{*}

képe ebben a nagyításban, tehát

B F_{2} = \frac{a}{a - c} \cdot B A^{*} = a = B A

alapján

A

-ban van, nagytengelye pedig ─ ami a pályának lineáris mérete:

\begin{matrix} \frac{a}{a - c} (k - c), \end{matrix}

ahogy az I. megoldásban is láttuk.

Megjegyzés. Szóljunk egyszer a helyes magyar beszédnek egy ide vágó eleméről is! Vannak a matematikának olyan kérdései, amelyek megoldásához közeledve ‐ példán folytatjuk ‐ helyes ez a beszédmód: az

X

pont egy olyan vonalon van rajta, amely

...

. A megoldás befejeződhet azzal, hogy az olyan vonalak közül kikeressük azt (vagy azokat), amely már minden tekintetben megfelel.
Ez kissé divatossá vált. Megvan azonban a közbeszédben is, idézhetnénk az irodalomból, már a múlt századból való példákat is. Csakhogy azoknak megvan a maguk megfelelő háttere!
Példánkban azonban nincs szükség erre, ez itt fölösleges köntörfalazás. Amilyen ez a szintén divatos bizonytalankodás: "

...

hát ezt én így mondanám

...

''. Tisztán látjuk, hogy csak egy olyan ellipszis van, ezt a magyar nyelv tömören így mondja, az az ellipszis,

...

.
Már halljuk az ellenvéleményt: az

A B

mint tengely körüli forgatással a térben végtelen sok olyan van. Akkor volna helyes ez a védekezés, ha 1. az előzmények alapján szó lehetne a térről, 2. utána igy zárná le a vitatkozó: egy olyan ellipszis, mégpedig az (az egyetlen), amely benne van a trapéz síkjában.
Pedig a trapéz síkjáról nem beszéltünk korábban! Mert természetesnek vesszük, hogy a feladat síkban értendő.
Ez a "háttér'' sok geometriai feladathoz hozzáértendő. Hanem ha valahol megbújik a szövegben valami kis említés síkról, akkor már a térre is gondolni kell ‐ azért, mert nem mondták ki, de céloztak rá.
(B. T.)