| Feladat: | F.2355 | Korcsoport: 18- | Nehézségi fok: nehéz |
| Füzet: | 1982/október, 63 - 64. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Skatulyaelv, Térgeometriai bizonyítások, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1982/február: F.2355 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás. Ha adott a térben egy pont és egy -t nem tartalmazó sík, a nem -en levő pontokat két osztályba sorolhatjuk aszerint, hogy -vel összekötve őket, -et metsző vagy -et nem metsző szakaszt kapunk-e. Belátható, hogy a tér -hez nem tartozó pontjainak ilyen kettévágása nem függ a pont megválasztásától. A kapott részeket nyílt féltereknek hívjuk, véges sok nyílt féltér közös részét pedig konvex poliédernek nevezzük, ha az korlátos és nem üres. (A tér valamely ponthalmazát korlátosnak mondjuk, ha van a térben olyan pont, és van olyan valós szám, hogy minden pontjának -től mért távolsága kisebb -nál.) Legyen tetszőleges konvex poliéder, és tekintsük a -t meghatározó síkokat. Ezek mindegyikéből a többiek egy‐egy konvex sokszöget metszenek ki, e sokszögeket hívjuk lapjainak. Lényeges, a konvexségből következő körülmény, hogy -nak minden síkon csak egy lapja van, és két lapjának csak egy közös oldala lehet. Legyen a -nak olyan lapja, amelynél több oldala egyetlen lapjának sincs. Jelöljük -nel oldalainak a számát, és tekintsük -lel szomszédos lapjait. Ezek oldalszáma csak 3 és közti egész szám lehet, a számuk viszont , így biztosan van köztük kettő, amelynek egyenlő az oldalszáma. II. megoldás. Felhasználjuk a konvex poliéderekre vonatkozó, Eulertől származó
Jelöljük az oldalszámú lapok számát -vel, akkor Ha , és az összegezést mindkét oldalon csak 6-ig végezzük el, a jobb oldalt csökkentjük többel, tehát 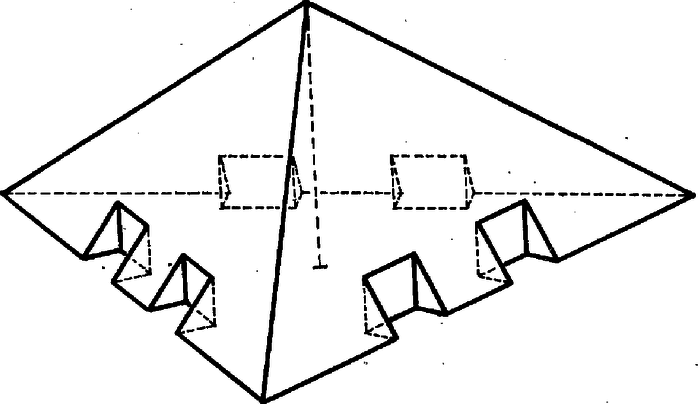 |