Kezdőlap


Feladat:	F.2354	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1982/november, 121 - 123. oldal		PDF \| MathML
Témakör(ök):	Trigonometriai azonosságok, Szögfelező egyenes, Terület, felszín, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1982/február: F.2354

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük az $A B C$ háromszög egymás utáni oldalaihoz tartozó szögfelező hosszát $A A' = f_{a}$ -val, $f_{b}$ -vel, $f_{c}$ -vel. Az $f_{a}$ két oldalán létrejött $A A' B$ és $A A' C$ háromszögek egy oldala közös, és $A$ -nál levő szögük egyenlő. Ezekből ajánlkozik: $f_{a}$ -ra abból írjunk fel egyenletet, hogy a részháromszögek területeinek összege egyenlő az eredeti háromszög területével (1. ábra):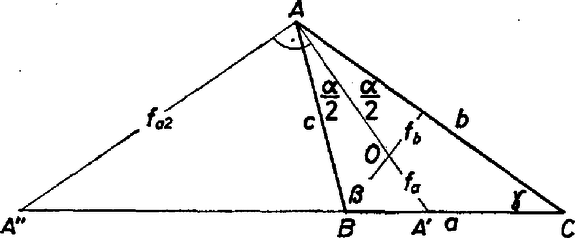

1. ábra

\begin{matrix} \frac{c + b}{2} f_{a} sin \frac{α}{2} = \frac{b c}{2} sin α . \end{matrix}

Innen a

sin 2 x = 2 sin x cos x

azonosság felhasználásával

\begin{matrix} f_{a} = \frac{2 b c}{b + c} cos \frac{α}{2}, \end{matrix}

eszerint azon múlik az állítás helyessége, hogy az adott háromszögben a félszögek cosinusai racionális számok-e vagy nem.
Mármost egy trigonometriai azonosság és a cosinustétel felhasználásával (és mert

α / 2

hegyesszög):

\begin{matrix} cos \frac{α}{2} = + \sqrt[]{\frac{1 + cos α}{2}} = + \sqrt[]{\frac{2 b c + (b^{2} + c^{2} - a^{2})}{4 b c}} = \sqrt[]{\frac{{(b + c)}^{2} - a^{2}}{4 b c}} = \\ = \sqrt[]{\frac{(b + c + a) (b + c - a)}{4 b c}} = \sqrt[]{\frac{378 \cdot 210}{4 \cdot 5^{3} \cdot 13^{2}}} = \frac{3 \cdot 21}{5 \cdot 13} (< 1), \end{matrix}

és ez racionális szám. Hasonlóan

\begin{matrix} cos \frac{β}{2} = \frac{3 \cdot 2^{2}}{13} (< 1) és cos \frac{γ}{2} = \frac{3}{5} (< 1) \end{matrix}

racionálisak. Ezzel bebizonyítottuk a feladat állítását.

II. megoldás. Legyen a beírt kör középpontja

O

, sugara

ϱ

, a háromszög területe

t

, kerülete

2 s

. Az

A A' C

háromszögben

C O

felezi a

C

-nél levő szöget, ezért a szögfelező felosztási arányára ismert tétel szerint

\begin{matrix} A O = \frac{C A}{C A + C A'} \cdot A A' = \frac{b}{b + \frac{b}{b + c} \cdot a} f_{a} (= \frac{b + c}{b + c + a} f_{a}), \end{matrix}

tehát

f_{a}

‐ számadataink mellett ‐ akkor és csak akkor racionális, ha

A O

mértékszáma racionális.

A O

O B_{1} = ϱ

és

A B_{1} = s - a = \frac{b + c - a}{2}

befogókkal meghatározott derékszögű háromszög átfogója.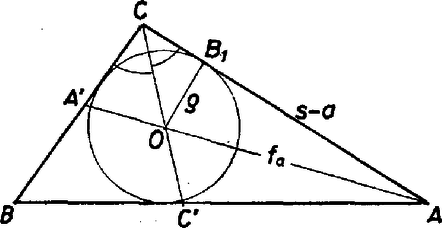

2. ábra

A Herón-féle területképlet felhasználásával

\begin{matrix} ϱ = \frac{t}{s} = \frac{1}{s} \sqrt[]{s (s - a) (s - b) (s - c)} = \sqrt[]{\frac{105 \cdot 64 \cdot 20}{189}} = \sqrt[]{\frac{100 \cdot 64}{9}} = \frac{80}{3}, \end{matrix}

és Pitagorasz tétele alapján

\begin{matrix} A O = \sqrt[]{{(\frac{80}{3})}^{2} + 105^{2}} = \frac{325}{3} . \end{matrix}

Ugyanígy

\begin{matrix} B O = \frac{208}{3} és C O = \frac{100}{3}, \end{matrix}

ezek szerint

f_{a}

, valamint

f_{b}

és

f_{c}

mértékszáma is racionális, amint a feladat állítja.

Megjegyzések. 1. A feladat kitűzésére az adott indítékot, hogy dr. Kelemen József, a miskolci műegyetem adjunktusa cikket tett közzé "A matematika tanítása'' című tanári folyóirat XXVIII. évfolyamának 1. számában (1981. február) az olyan háromszögekről, amelyeknek oldalai és szögfelezői racionális számok. Tétele: egy háromszögnek akkor és csak akkor racionálisak az oldalai és a szögfelezői, ha az oldalak előállíthatók a következő alakban:

\begin{matrix} a = r (p - q) (1 + p q) ({(1 + p q)}^{2} - {(p - q)}^{2}), \\ b = r q (1 - q^{2}) {(1 + p^{2})}^{2}, \\ c = r p (1 - p^{2}) {(1 + q^{2})}^{2}, \end{matrix}

ahol

p

q

és

r

pozitív racionális számok és

q < p < 1

. Példánkban a paraméterek

p = 2 / 3

és

q = 1 / 2

voltak, és

r = 216

mellett az oldalak mértékszámai egészek lettek.
A cikkben a következő összefüggés is megtalálható:

\begin{matrix} t = \frac{(a + b) (a + c) (b + c) f_{a} f_{b} f_{c}}{8 a b c s} . \end{matrix}

A paraméterek jelentése

\begin{matrix} p = tg \frac{α + β}{4}, q = tg \frac{β}{4} . \end{matrix}

Ezekböl következik, hogy

(α + β) / 2

-nek és

β / 2

-nek mindegyik szögfüggvénye racionális, tehát

α / 2

-nek is,

γ / 2

-nek is, hiszen ─ mint ismeretes,

tg x / 2 = u

jelöléssel

\begin{matrix} sin x = \frac{2 u}{1 + u^{2}}, cos x = \frac{1 - u^{2}}{1 + u^{2}}, tg x = \frac{2 u}{1 - u^{2}}, \end{matrix}

(az utóbbi csak akkor, ha

u \neq \pm 1

).
A háromszög eredeti szögeinek szögfüggvényei már

\begin{matrix} sin α = \frac{2 t}{b c}, cos α = \frac{b^{2} + c^{2} - a^{2}}{2 b c}; \end{matrix}

alapján is racionálisak (ha

cos α \neq 0

).
Ezek alapján az

A A'' = f_{a 2}

külső szögfelező is racionális, mert

A A'' C - A A'' B = A B C

f_{a 2} = \frac{2 b c}{b - c} sin \frac{α}{2}

2. Mindezek szerint a vizsgált háromszög-osztály különleges részét alkotja a Herón-háromszögek osztályának, amelynek jellemzése:

a

b

c

és

t

racionális. Ezekből

tg α / 2

tg β / 2

tg γ / 2

is racionális, de pl.

sin α / 2

cos α / 2

magában általában nem. (A vizsgált osztály háromszögeit mindegyik szögfelező két heróni részháromszögre osztja.)