Kezdőlap


Feladat:	F.2330	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1982/március, 113 - 115. oldal		PDF \| MathML
Témakör(ök):	Műveletek helyvektorok koordinátáival, Hossz, kerület, Szabályos sokszögek geometriája, Feladat, Síkgeometriai bizonyítások, Középponti és kerületi szögek
Hivatkozás(ok):	Feladatok: 1981/október: F.2330

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Toljuk el mindegyik $\vec{M_{i} N_{i}}$ -t kezdőpontjánál fogva $M$ -be, az ${\vec{M N'}}_{i}$ helyzetbe. Mindegyik $N'_{i}$ végpont rajta van az $M N$ átmérőjű $k$ Thalész-körön, hiszen $M N'_{i} ∥ M_{i} N_{i} ⊥ N N_{i}$ , illetve akkor is, ha az $M M_{i} N_{i} N'_{i}$ derékszögű négyszög valamelyik oldala 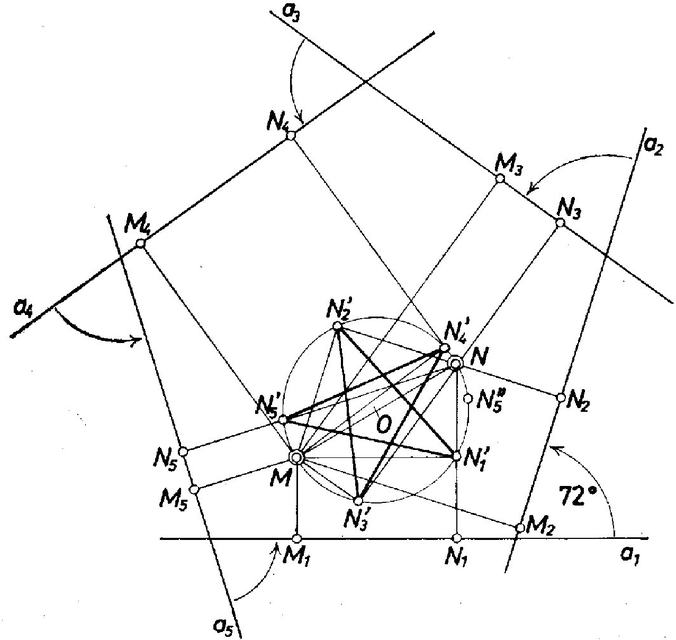$0$ .
Továbbá az $N'_{i} M N'_{i + 1}$ és $N'_{5} M N'_{1}$ irányított szögek értéke $72^{\circ}$ vagy $72^{\circ} + 180^{\circ}$ , amekkora forgás $a_{i}$ -t $a_{i + 1}$ -be, illetve $a_{5}$ -öt $a_{1}$ -be átviszi ( $i = 1$ , $2$ , $3$ , $4$ ).

Ezekből a kerületi és középponti szögek összefüggése alapján adódik, hogy az

N'_{i} O N'_{i + 1}

és

N'_{5} O N'_{1}

irányított szögek értéke

2 \cdot 72 = 144^{\circ}

(+ 360^{\circ})

, ahol

O

k

középpontja, tehát

N'_{1} N'_{2} N'_{3} N'_{4} N'_{5}

k

-ba írt szabályos csillagötszög (körüljárási iránya egyező az

a_{1}

a_{2}

...

oldalegyenesek körüljárásával), más szóval

N'_{1} N'_{4} N'_{2} N'_{5} N'_{3}

k

-ba írt konvex szabályos ötszög. Ezekkel az állítás bal oldalából, egymás utáni alakításokkal

\begin{matrix} 2 (\vec{M_{1} N_{1}} + \vec{M_{2} N_{2}} + \vec{M_{3} N_{3}} + \vec{M_{4} N_{4}} + \vec{M_{5} N_{5}}) = \\ = 2 (\vec{M N'_{1}} + \vec{M N'_{2}} + \vec{M N'_{3}} + \vec{M N'_{4}} + \vec{M N'_{5}}) = \\ = 2 (\vec{M O} + \vec{O N'_{1}} + \vec{M O} + \vec{O N'_{2}} + \vec{3 M O} + \vec{O N'_{3}} + \vec{O N'_{4}} + \vec{O N'_{5}} = \\ = 10 \cdot \vec{M O} + 2 ({\underset{︸}{\vec{O N'_{1}} + \vec{O N'_{2}}}}_{}^{} + {\underset{︸}{\vec{O N'_{3}} + \vec{O N'_{4}}}}_{}^{} + \vec{O N'_{5}}) = 5 \vec{M N} \end{matrix}

‐ ahogy a feladat állítja ‐ ugyanis az utolsó zárójelben álló összeg 2‐2 tagját összeadva

\begin{matrix} \vec{O P_{12}} + \vec{O P_{34}} + \vec{O N'_{5}} = \vec{O N''_{5}} + \vec{O N'_{5}} = 0, \end{matrix}

ahol

P_{12}

O N'_{4}

szakaszon,

P_{34}

O N'_{1}

-n van,

N_{2} P_{12} ∥ O N'_{1}

és

N'_{3} P_{34} ∥ {O N'}_{4}

, végül

N''_{5}

a rövidebbik

N'_{1} N'_{4}

körív felezőpontja, vagyis

k

-nak az

N'_{5}

-vel átellenes pontja, hiszen itt metszi egymást

N'_{2} P_{12}

és

N'_{3} P_{34}

K. L.

II. megoldás. Válasszuk a koordináta-rendszer

x

tengelyéül

a_{5}

-öt, ekkor az

a_{i}

egyenes irányszöge

i \cdot 72^{\circ}

. Legyen másrészt az

M N

félegyenes irányszöge

φ

, ekkor a vetületek előjellel vett hosszai

\begin{matrix} M_{i} N_{i} = M N cos (φ - i \cdot 72^{\circ}), \end{matrix}

a_{i} - n

pozitívnak vesszük az

a_{i - 1}

-gyel való metszésponttól az

a_{i + 1}

-gyel való metszéspont felé mutató irányt.
Bontsuk mindegyik

\vec{M_{i} N_{i}}

-t

a_{5}

irányú és rá merőleges komponensekre, és összegezzük külön-külön a komponenseket. Alkalmazni fogjuk a következő két azonosságot :

\begin{matrix} 2 cos u cos v = cos (u - v) + cos (u + v), \\ 2 cos u sin v = sin (u + v) - sin (u - v) . \end{matrix}

Az állítás bal oldalán álló összeg

a_{5}

irányú komponense

\begin{matrix} 2 \sum_{i = 1}^{5} \vec{M_{i} N_{i}} cos i \cdot 72^{\circ} = \vec{M N} \sum_{i = 1}^{5} cos (φ - i \cdot 72^{\circ}) cos i 72^{\circ} = \\ = \vec{M N} \sum_{i = 1}^{5} cos (φ - i \cdot 144^{\circ}) + 5 \vec{M N} cos φ . \end{matrix}

Itt a második tag az állítás jobb oldalán álló vektor vetülete, az első kifejezés értéke pedig

0

, ugyanis az addíciótétel szerint

\begin{matrix} cos φ \sum_{i = 1}^{5} cos i \cdot 144^{\circ} + sin φ \sum_{i = 1}^{5} sin i \cdot 144^{\circ}, \end{matrix}

és az újabb összegek értéke külön-külön is

0

, hiszen

576^{\circ} = 720^{\circ} - 144^{\circ}

és

432^{\circ} = 720^{\circ} - 288^{\circ}

\begin{matrix} 2 cos 144^{\circ} + 2 cos 288^{\circ} + cos 0^{\circ} = 2 (- \frac{\sqrt[]{5} + 1}{4} + \frac{\sqrt[]{5} - 1}{4}) + 1 = 0, \end{matrix}

illetve

\pm sin 144^{\circ} \pm sin 288^{\circ} + sin 0^{\circ} = 0.

A bal oldali összegnek

a_{5}

-re merőleges összetevője pedig hasonlóan

\begin{matrix} 2 \sum_{i = 1}^{5} \vec{M_{i} N_{i}} sin i \cdot 72^{\circ} = 5 \vec{M N} sin φ - \vec{M N} \sum_{i = 1}^{5} sin (φ - i \cdot 144^{\circ}), \end{matrix}

és itt a második kifejezés

0

.
Az állítás két oldalának két, egymásra merőleges irányú komponensei megegyeznek. Ezzel bebizonyítottuk az állítás helyességét.

Megjegyzés. Ha rögzítjük

M

-et és belátjuk az állítást két alkalmasan választott

N

-re, akkor az állítás a rögzített

M

mellett abból következik, hogy most már az

M N

vektor felbontható a már megvizsgált két

M N

vektor lineáris kombinációjára, és az állításban szereplő lépéseken könnyű végigkövetni e felbontás hatását. Végül

M

rögzített voltától úgy szabadulhatunk meg, hogy a tetszőleges

M N

vektort az

M_{0} N

és

M_{0} M

vektorok különbségeként állítjuk elő, ahol

M_{0}

a rögzített vektor. Elég tehát az állítást arra az esetre belátni, ha

M N

például az ötszög egyik oldala, átlója, vagy a centrumból valamelyik csúcsig futó szakasz.