Kezdőlap


Feladat:	F.2294	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1981/október, 63 - 64. oldal		PDF \| MathML
Témakör(ök):	Geometriai egyenlőtlenségek, Feladat, Síkgeometriai bizonyítások
Hivatkozás(ok):	Feladatok: 1981/január: F.2294

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük az $a$ , $b$ , $c$ oldalú háromszög $c$ -hez tartozó súlyvonalának hosszát $s_{c}$ -vel. Bizonyítandó, hogy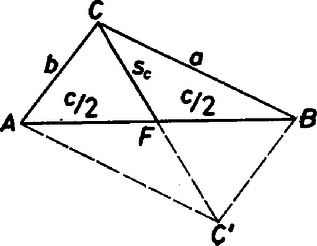

\begin{matrix} \frac{c^{2} - {(a - b)}^{2}}{2 (a + b)} \leq a + b - 2 s_{c} < \frac{c^{2} + {(a - b)}^{2}}{4 s_{c}} . \end{matrix}

(1)

Megoldás. A feladat eredeti kitűzésében sajtóhiba volt. Itt a fenti állítást bizonyítjuk. (Az eredetiben a jobb oldali számláló tagjai között

+

jel állt, és ez az egyenlőtlenség jobb oldali felének bizonyítását még könnyítette. Bemutatjuk egy könnyű számpéldán, milyen torzítást jelent ez. A

34

56

78

oldalakkal bíró háromszög esetében

c

-nek

56

-ot véve a számláló helyesen

1200

, tévesen

5072

, vagyis több mint

4

-szer akkora.)
Tükrözzük az

A B C

háromszöget az

A B = c

oldal

F

felezőpontjára a

B A C'

helyzetbe. Így paralelogrammát kapunk, átlói

c

és

C C' = 2 s_{c}

, oldalai

a

és

b

Ismeretes, hogy paralelogramma átlóinak négyzetösszege egyenlő az oldalak négyzetösszegével. Ebből a

\begin{matrix} c^{2} = 2 a^{2} + 2 b^{2} - 4 s_{c}^{2} \end{matrix}

kifejezést a számlálókba helyettesítve, egyszerű átrendezéssel ez adódik:

\begin{matrix} {(a + b)}^{2} - 4 s_{c}^{2} = (a + b - 2 s_{c}) (a + b + 2 s_{c}), \end{matrix}

vagyis az első tényező azonos a kettős egyenlőtlenség közepén álló kifejezéssel.
Írjuk föl a háromszög-egyenlőtlenséget a

C C' A

háromszög

C C'

oldalára:

\begin{matrix} a + b > 2 s_{c} \end{matrix}

(2)

Eszerint az (1) közepén álló kifejezés minden valódi háromszögben pozitív. Ezzel osztva (1)-et, elég bizonyítanunk a vele ekvivalens következőt:

\begin{matrix} \frac{(a + b) + 2 s_{c}}{(a + b) + (a + b)} ≦ 1 < \frac{(a + b) + 2 s_{c}}{2 s_{c} + 2 s_{c}} . \end{matrix}

Ez pedig (2) szerint helyes, és egyenlőség nem állhat fenn, hiszen a bal oldali számláló csökkentéssel állt elő a nevezőjéből, a jobb oldali számláló pedig növeléssel a maga nevezőjéből.