Kezdőlap


Feladat:	F.2289	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Hetyei Gábor
Füzet:	1981/május, 199 - 201. oldal		PDF \| MathML
Témakör(ök):	Geometriai egyenlőtlenségek, Indirekt bizonyítási mód, Egyéb sokszögek geometriája, Feladat
Hivatkozás(ok):	Feladatok: 1980/december: F.2289

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ellentmondásra jutunk annak föltételezéséből, hogy az $A D$ , $B E$ , $C F$ átlók mindegyike nagyobb 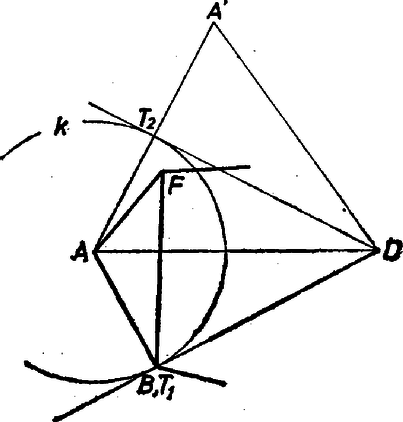$2$ -nél.
Legyen $A D > 2$ , és rajzoljuk meg $A$ körül az egységnyi sugarú $k$ kört. Az $A$ -val szomszédos $B, F$ csúcsok benne vannak $k$ -ban vagy éppen a kerületén, emiatt a $B F$ szakasz $D$ -ből vett látószöge nem lehet nagyobb, mint a $D$ -ből $k$ -hoz húzott érintők közti $T_{1} D T_{2}$ szög, ahol $T_{1}, T_{2}$ az érintési pontok.

1. ábra

Belátjuk, hogy

\begin{matrix} B D F ∢ ≦ T_{1} D T_{2} ∢ < 60^{\circ} . \end{matrix}

Fordítsuk el az

A D T_{1}

háromszöget

D

körül úgy, hogy

T_{1}

essék egybe

T_{2}

-vel, és legyen ekkor

A

új helyzete

A'

. Az

A D A'

háromszögben

A D = A' D > 2

és

A A' ≦ A T_{2} + T_{2} A' = A T_{2} + T_{1} A = 2 < A D

, ezért a háromszög

D

-nél levő szöge kisebb a másik kettőnél, amelyek egyenlők, tehát kisebb

60^{\circ}

-nál. Ámde

\begin{matrix} A D A' ∢ = A D T_{2} ∢ + T_{2} D A' ∢ = A D T_{2} ∢ + T_{1} D A ∢ = T_{1} D T_{2} ∢, \end{matrix}

állításunkat ezzel igazoltuk.
Ha mármost egyidejűen

A D

E B

és

C F

mindegyike nagyobb volna, mint

2

‐ vagyis mint konvex hatszögünk akármelyik oldalának a 2-szerese ‐, akkor meggondolásunkban

D

szerepét sorra

B

-nek,

F

-nek átadva ‐ egyidejűen

A

szerepét a szemben levő csúcsnak ‐, azt kapnánk, hogy a

B D F

háromszög szögeinek összege kisebb

180^{\circ}

-nál, hiszen külön-külön mindegyik kisebb, mint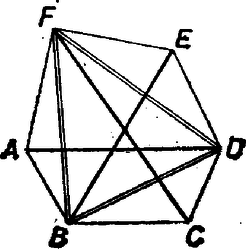

60^{\circ}

2. ábra

Ez az ellentmondás mutatja a feladat állításának helyességét.

Hetyei Gábor (Pécs, Leőwey K. Gimn., II. o. t.)

Megjegyzések. 1. Tetszetős ötlet a 3. ábra szerinti hatszög minden második oldalát meghosszabbítani, és így egy háromszögbe belefoglalni az idomot, számos dolgozat ebből indult ki.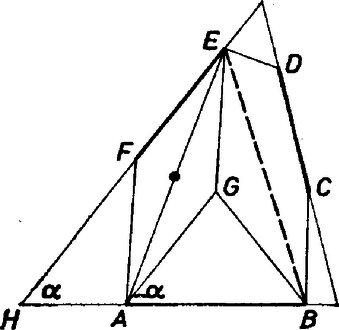

3. ábra

Kiválasztva a háromszög legkisebb szögét ‐ vagy az ilyenek egyikét, ha több van, az ábrán

A H F ∢ = α

ilyen ‐, erre

α ≦ 60^{\circ}

. Ekkor az

A H F

szög mindkét szárára rátámaszkodó

B E

átló nem hosszabb, mint

2

egység.
Tükrözzük

F

-et az

A E

szakasz felezőpontjára, legyen a képe

G

. Így egyrészt az

A F E G

négyszög paralelogramma, másrészt

G A B ∢ = F H A ∢ = α ≦ 60^{\circ},

tehát

E G = F A ≦ 1

, illetve az

α

-val szemben levő

G B

oldalnál van nagyobb az

A G = F E ≦ 1

és

A B ≦ 1

oldalak közt, ti. az, amelyikkel szemben

α

-nál nagyobb szög van ; esetleg

A G = A B = G B

. Eszerint

G B ≦ 1

, ennélfogva a

G B E

háromszögből

E B ≦ E G + G B ≦ 2

. Egyenlőség előfordulhat, ha a

G B E

háromszög elfajult, és egyidejűen a hatszög felhasznált két oldala éppen

1

-gyel egyenlő. ‐ Ezzel a feladat állítását az ábrán fölvett hatszögre bebizonyítottuk.
Könnyen kiegészítheti az olvasó a fentieket az olyan hatszögek vizsgálatával, amelyekben sem a 3. ábrabeli meghosszabbítások révén nem keletkezik befoglaló háromszög, sem a

B C

D E

F A

oldalhármas használatával. Ha ugyanis pl. az

A B

félegyenes irányát a

C D

félegyenes irányába átvivő forgás (a

B C

irányán át gondoljuk) szöge éppen

180^{\circ}

vagy több is annál, akkor a fenti háromszög

2

oldalegyenese párhuzamos, vagy pedig az

E F

oldalával kívülről támaszkodik a hatszög a létrejövő háromszög egyik oldalához. És egyidejűleg az is fennállhat, hogy a

B C

félegyenest a

D E

irányába legalább

180^{\circ}

-nyi elfordulás viszi át (4. ábra). ‐ Ebből a két "sikertelenségből'' levont következtetésekkel lehet bizonyítani az állítást a szóban forgó átlók valamelyikére. (Vagyis "megfoltozni'' az eddig hiányos bizonyítást.)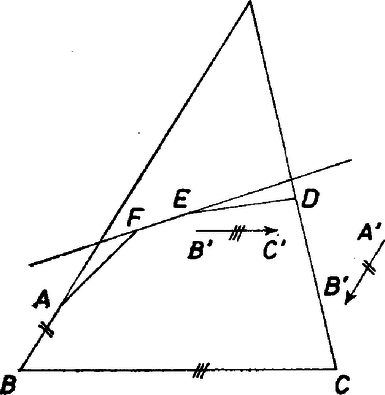

4. ábra

2. Versenybizottságokban gyakran elhangzik ilyen bírálat: nem teljes, de könnyen kiegészíthető teljessé. Ezt a keveset azonban ‐ amilyenre példa az előbbi megjegyzés ‐ csak akkor toldják hozzá a versenyző munkájához, ha van nyoma annak, hogy érezte az illető: valami még hátra van. Más szóval, ha nem tekintette befejezettnek a bizonyítást abban a hiányos állapotban.
3. Még egy tanulság a 3. ábrához: ne csak egy ábrát rajzoljunk, és ne csak alig-alig eltérőt valami szabályostól, mert az ilyesmi nem szerénység, hanem szűklátókörűség!