Feladat: F.2276 Korcsoport: 18- Nehézségi fok: átlagos
Megoldó(k):  Bali J. ,  Breiner L. ,  Terenyi Zoltán ,  Tranta Beáta 
Füzet: 1981/március, 109 - 110. oldal  PDF  |  MathML 
Témakör(ök): Kombinatorikus geometria síkban, Körök, Feladat
Hivatkozás(ok):Feladatok: 1980/október: F.2276

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Jelöljük az adott pontot P-vel, a tőle legtávolabb levő körközéppontot O1-gyel (illetve ha több ilyen van, ezek bármelyikét); az O1 közepű kört k1-gyel. Ekkor minden adott kör középpontja a P körüli, PO1 sugarú c1 körben van vagy ennek határvonalán. (A "cirkulus'' szó kezdőbetűjével további nem az adottak közül való köröket fogunk jelölni.)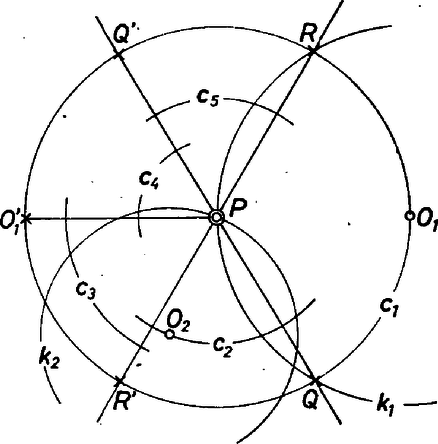


Messe c1 a k1-et a Q és R pontban, és legyen Q, O1, R tükörképe P-re Q', O1', R'. A k1 kör lefed minden olyan körközéppontot, amely a QPR konvex körcikkbe esik, beleértve ennek határát is. A PR', PO'1, PQ' sugarak c1 hátra levő részét 4 további körcikkre osztják, nyílásszögük 60∘. Megmutatjuk, hogy az ezekbe eső középponthalmazok lefedésére is található egy‐egy alkalmas kör az adottak közül. Elég ezt például a PQR'=S körcikkre belátni, hozzá értve a PQ, PR' sugarakat is; a további három körcikkben ugyanezt a gondolatmenetet alkalmaznánk.
Föltehetjük, hogy a kiszemelt S szektorban van adott középpont, hiszen ha sem ebben, sem a többi 3-ban nem volna, máris készen volnánk. Legyen az S-beli körközéppontok közül a P-től legtávolabbi ‐ vagy egy az ilyenek közül ‐ O2, ekkor az S-beli középpontok benne vannak a QPR' szögtartománynak abban a részében is, amely a P körüli, O2-n átmenő c2 körnek is a belsejébe esik vagy a határára. Ezt a részt pedig nyilván lefedi az O2 körüli adott k2 kör.
Ezzel bebizonyítottuk az állítást.
 

 Terenyi Zoltán (Jászberény, Lehel Vezér Gimn., IV. o. t.)
 

Megjegyzések: 1. A megoldásban nem használtuk ki, hogy pontosan 1980 db körünk van, csak azt, hogy véges sok.
2. Könnyen látható, hogy 4 kör nem mindig tehet eleget a követelménynek, pl. abban az esetben, ha 5 középpont szabályos ötszöget alkot P középponttal, a többi n-5 középpont pedig P-hez "közel'' van.
3. Fontos az is, hogy lehet egy középpont valamelyik kiválasztott körnek a határán is, mert különben ha 6 középpont szabályos hatszöget alkot P középponttal, és nincs nagyobb az adott körök között, mint ez a 6, akkor nem teljesülne a követelmény.