Kezdőlap


Feladat:	F.2272	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Danyi Pál
Füzet:	1981/március, 104 - 105. oldal		PDF \| MathML
Témakör(ök):	Sorozat határértéke, Feladat
Hivatkozás(ok):	Feladatok: 1980/október: F.2272

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A bogár lépései során felváltva hol az első, hol a második koordinátáját változtatja meg. Páratlan sorszámú lépéseivel az első koordinátáját módosítja, mégpedig mindig az ellentétes irányban és negyedakkora mértékben, mint közvetlenül előtte. Emiatt az első koordináta $k$ módosítása, tehát a $(2 k - 1)$ -edik lépés után az első koordinátája

\begin{matrix} x_{2 k - 1} = 1 - \frac{1}{4} + ... + {(- \frac{1}{4})}^{k - 1} = \frac{1 - {(- \frac{1}{4})}^{k}}{1 - (- \frac{1}{4})} \end{matrix}

lesz, és ugyanennyi marad az értéke a

2 k

-adik lépés után is.
A második koordináta hasonlóan változik, a

2 k

-adik lépés után az értéke

\begin{matrix} y_{2 k} = \frac{1}{2} - \frac{1}{8} + ... + \frac{1}{2} {(- \frac{1}{4})}^{k - 1} = \frac{1}{2} x_{2 k - 1}, \end{matrix}

és ugyanennyi marad az értéke a

(2 k + 1)

-edik lépés után is. Mivel 4 egymás utáni hatványai különböző egész számok, közülük a

k

-adik nagyobb a

k

-adik pozitív egésznél, vagyis

4^{k} > k

. Emiatt

4^{k}

minden határon túl nő, ha

k

befutja a pozitív egészeket, és

4^{- k}

0

-hoz tart. Tehát

x_{n}

határértéke 4/5, és

y_{n}

határértéke ennek fele, 2/5.

Jelöljük

B_{n}

-nel az

(x_{n}; y_{n})

és

B

-vel a

(\frac{4}{5}; \frac{2}{5})

pontot. Mivel

B_{n}

és

B

távolsága kisebb az

| x - x_{n} | + | y - y_{n} |

összegnél, és ez az utóbbi 0-hoz tart, a bogár a

B (\frac{4}{5}; \frac{2}{5})

pontot közelíti meg egyre jobban.

II. megoldás. Jelöljük továbbra is

B_{n}

-nel a bogár helyzetét az

n

-edik lépés után, és

B_{0}

-lal az origót.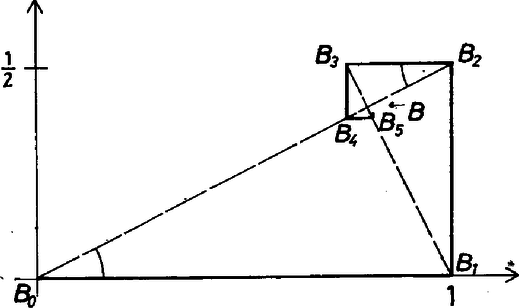

B_{n} B_{n + 1} B_{n + 2}

háromszögek

n = 0

, 1, 2,

...

mellett mind hasonlóak, hiszen derékszögűek, és a

B_{n} B_{n + 1}

B_{n + 1} B_{n + 2}

befogók aránya

n

-től függetlenül

2 : 1

. Nevezetesen a

B_{0} B_{1} B_{2}

B_{2} B_{3} B_{4}

háromszögekben a

B_{0}

-nál, illetve

B_{2}

-nél levő szögek egyenlőek, és száraik ellentétes irányításúak. Emiatt az átfogóik egyenese azonos,

B_{4}

rajta van a

B_{0} B_{2}

szakaszon. Hasonlóan kapjuk, hogy

B_{5}

rajta van a

B_{1} B_{3}

szakaszon, vagyis a

B_{4} B_{5}

szakasz a

B_{0} B_{2}

B_{1} B_{3}

szakaszok

B

metszéspontjából, mint centrumból való

16 : 1

arányú kicsinyítéssel is megkapható a

B_{0} B_{1}

szakaszból. Innen kezdve pedig az egész pálya folytatása megkapható úgy, hogy a

B_{0} B_{1} B_{2} B_{3} B_{4}

törött vonalra alkalmazzuk ezt a kicsinyítést, majd a kapott eredményre is alkalmazzuk, és így tovább. Más szavakkal elmondva ugyanezt, azt kapjuk, hogy ha a

T_{0} = B_{0} B_{1} B_{2} B_{3} B_{4}

törött vonalra a

B

centrumból rendre

16^{k} : 1

arányú kicsinyítést alkalmazunk, akkor éppen a

T_{k} = B_{4 k} B_{4 k + 1} B_{4 k + 2} B_{4 k + 3} B_{4 k + 4}

törött vonalat kapjuk. Mivel a

T_{0}

törött vonal pontjai közül

B_{0}

van

B

-től legmesszebb, ebből kapjuk, hogy

T_{k}

pontjai

B

-től legfeljebb

B_{0} B / 16^{k}

távolságra vannak. Mivel ez 0-hoz tart (amit ugyanúgy láthatunk be, mint az I. megoldásban azt, hogy

1 / 4^{k}

tart 0-hoz, bár egyszerűen ez utóbbi állításból is kiolvasható), ebből következik, hogy a bogár mind jobban közeledik a

B

ponthoz.

B_{0} B_{2}

egyenes egyenlete

y = x / 2

, a

B_{1} B_{3}

-é

y = 2 (1 - x)

, emiatt ezek metszéspontjában

x = 4 / 5

y = 2 / 5

, tehát

B

koordinátéi

(\frac{4}{5}; \frac{2}{5})

Danyi Pál (Pécs, Nagy Lajos Gimn., II. o. t.)