| Feladat: | F.2266 | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Megoldó(k): | Molnár Jenő , Poppe András | ||
| Füzet: | 1981/január, 11 - 12. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Egyéb szinezési problémák, Kombinációk, Szabályos sokszögek geometriája, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1980/szeptember: F.2266 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás. A szabályos -szög csúcsai között biztosan van két szomszédos egyforma színű, mondjuk kék, mivel a csúcsok száma páratlan. Legyen ez a két csúcs és (1. ábra). 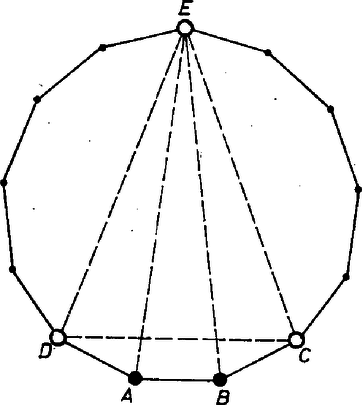 1. ábra Ha a velük szomszédos csúcsok ‐ és ‐ valamelyike kék, akkor máris van három egyszínű csúcs, melyek egyenlő szárú háromszöget alkotnak. Ha az oldal felező merőlegesén fekvő csúcs színe kék, akkor szintén van olyan háromszög, amilyet keresünk. Végül ha ezek egyike sem következett be, akkor , és mindegyike piros, azaz most is van egy egyenlő szárú háromszög egyező színű csúcsokkal. Molnár 724 Jenő (Nagykanizsa, Landler J. Gimn., III. o. t.) II. megoldás. Tekintsünk 7 egyszínű csúcsot a -szög csúcsai közül (7 egyező színű csúcs mindig található). Összesen olyan egyenes szakasz van, amelyeknek ezek a csúcsok a végpontjai. Mivel a szabályos 13-szög csúcsai között csak 6 különböző hosszúságú szakasz húzható, ezért a 21 szakasz között van legalább 4, amelyek hossza egyenlő. Mivel ezek 7 pontot kötnek össze, ezért nem lehet minden végpontjuk különböző. Egyenlő hosszúságú szakaszok csatlakozása esetén viszont egyenlő szárú háromszög keletkezik, melynek csúcsai az előzőek értelmében egyező színűek. Poppe András (Budapest, Könyves Kálmán Gimn., IV. o. t) Megjegyzések. Számozzuk meg a 13-szög csúcsait 1-től 13-ig, és osszuk ezeket a számokat két csoportba aszerint, hogy a nekik megfeleltetett csúcs piros vagy kék. Az 1872. gyakorlat megoldásában (1980. május, 209. oldal) megmutattuk, hogy legalább az egyik csoportban található 3 szám, , , , melyek számtani sorozatot alkotnak. Az ezeknek megfelelő csúcsok egyszínűek, és nyilván egyenlő szárú háromszöget határoznak meg. Van der Waerden (1903‐) holland matematikus egy nevezetes tétele szerint minden és egész számhoz található olyan , hogy akárhogyan is osztjuk csoportba az -től -ig terjedő egészeket, legalább az egyik csoport tartalmaz tagú számtani sorozatot. Így például minden -hoz van olyan , hogy akárhogyanis színezzük ki színnel a szabályos -szög csúcsait, mindenképpen ki tudunk választani 3 egyszínű csúcsot, melyek egyenlő szárú háromszöget alkotnak. 2. A feladat állítása igaz marad, ha 13 helyébe 5-öt, 7-et, vagy tetszőleges 8-nál nagyobb egész számot mondunk. A 3, 4, 6 és 8-szögek csúcsait viszont lehet úgy pirosra és kékre színezni, hogy ne alkossanak egyszínű egyenlő szárú háromszöget. 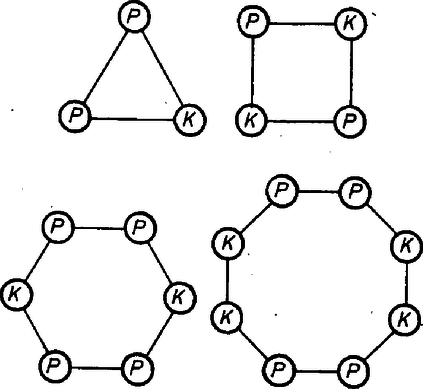 2. ábra |