Kezdőlap


Feladat:	F.2264	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bán L. , Benedek Ágnes , Csere K. , Csikós Zs. , Czakó F. , Elter J. , Erdős 205 J. , Feledi Gy. , Fodor L. , Fritz P. , Görög I. , Heckenast L. , Horváth 302 A. , Horváth 718 I. , Kántor Zs. , Kappelmayer Hedvig , Kelemen B. , Kiss 352 Gy. , Kiss E. , Kurusa Á. , Megyeri L. , Simon K. , Sz. Nagy Cs. , Szabó T. , Szegedy Patrik , Takáts L. , Tranta Beáta , Vajnai A. , Weisz F.
Füzet:	1980/november, 138 - 139. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Síkgeometriai számítások trigonometria nélkül háromszögekben, Szabályos sokszögek geometriája, Feladat, Középponti és kerületi szögek
Hivatkozás(ok):	Feladatok: 1980/május: F.2264

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A $k$ körbe írt $O_{1} O_{2} ... O_{7}$ szabályos hétszög csúcsai közül választott $O_{1} O_{2} O_{4}$ háromszög szögeire a kerületi szögek tétele szerint $O_{4} ∢ : O_{1} ∢ : O_{2} ∢ = 1 : 2 : 4$ . Jelöljük szögfelezőinek a szemben fekvő oldallal való metszéspontját rendre $F_{4}$ , $F_{1}$ , $F_{2}$ -vel, $F_{2}$ -t nyilván az $O_{2} O_{6}$ húr metszi ki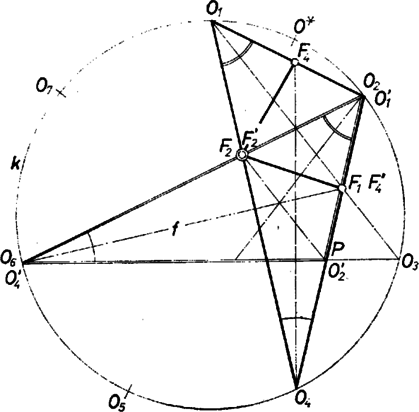, $F_{1}$ -et pedig $O_{1} O_{3}$ .
Mivel még $O_{2} O_{6} = O_{1} O_{4}$ , azért $F_{2}$ az $O_{1} O_{2} O_{4} O_{6}$ szimmetrikus trapéz átlóinak metszéspontja. Eszerint az $O_{1} O_{4} O_{2}$ háromszög elfordítható $F_{2}$ körül úgy, hogy $O_{1}$ , $O_{4}$ rendre $O_{2}$ , $O_{6}$ -ba jusson; forduljon egyidejűleg $O_{2}$ a $P$ pontba. $O_{6} O_{2} P ∢ = O_{4} O_{1} O_{2} ∢ = O_{6} O_{2} O_{4} ∢$ , a forgási irányokat is beleértve, ezért $P$ az $O_{2} O_{4}$ húron van, továbbá ugyanígy az $O_{6} O_{3}$ húron is, ezek metszéspontja.

Jelöljük az

X

pont ilyen forgatottját

X'

-vel (vagyis

O'_{1} O'_{2} O'_{4} = O_{2} P O_{6}

), és tekintsük az

F'_{2}

F'_{4}

pontokat.

F'_{2} = F_{2}

, helyben maradt. Az

O_{6} F'_{4} = f

felező felezi az

O_{2} O_{3}

ívet, tehát átmegy

k

középpontján. Így

F'_{4}

azonos

F_{1}

-gyel, egymás tükörképei

f

-re, hiszen

F'_{4}

P O_{2}

oldalon, vagyis az

O_{4} O_{2}

egyenesen van, és ez az

O_{1} O_{3}

egyenes, az

O_{1} F_{1}

felező képe. Eszerint

F_{2} F_{1} = F'_{2} F'_{4} = F_{2} F_{4}

, az

F_{2} F_{1} F_{4}

háromszög valóban egyenlő szárú.

Szegedy Patrik (Budapest, Fazekas M. Gyak. Gimn., IV. o. t.)

II. megoldás. Legyenek az

A B C

háromszög szögei az adott aránypárok sorrendjében

α

β

γ

, a csúcsukból induló szögfelezők által a szemben fekvő oldalból kimetszett pontok rendre

D

B C

-ből),

E

és

F

. Szemlélet és mérés szerint

F D = F E

, ezt bizonyítjuk.
Az arányt visszafelé olvasva

γ / 2 = β

, tehát egyrészt a

B C F

háromszög egyenlő szárú:

B F = C F

, másrészt

F C A ∢ = F B C ∢

; így elég lenne azt belátni, hogy az

F B D

háromszög ráfordítható az

F C E

háromszögre. A

C E = B D

egyenlőséget bizonyítjuk, felhasználva az aránybeli és a szerkesztésbeli felezésekből eredő hasonlóságokat.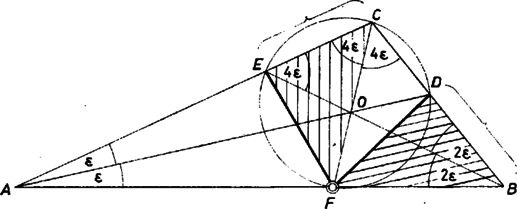

Jelöljük a szögfelezők metszéspontját

O

-val. Tekintsük a hasonló háromszögekből alakított alábbi párokat, alattuk zárójelben az egymás utáni szögek mértékszámai állnak, alkalmi egységnek választva az

ε = 180^{\circ} / 14

-et. Írjuk alájuk megfelelő oldalpárjaik arányaiból 2‐2-nek az egyenlőségét, szorozzuk össze a bal, valamint a jobb oldalakat és egyszerűsítsünk:

\begin{matrix} B D A ▵ \sim C O A ▵ & C E B ▵ \sim O C B ▵ & O C B ▵ \sim C B A ▵ \\ (4 : 9 : 1) & (8 : 4 : 2) & (8 : 4 : 2) \\ \frac{B D}{C O} = \frac{B A}{C A}, & \frac{B C}{C E} = \frac{B O}{O C}, & \frac{B O}{A C} = \frac{B C}{A B}, \\ \frac{B D}{C E} = 1. \end{matrix}

Ezt akartuk bizonyítani, és ezzel a feladat állítását is bebizonyítottuk.

Megjegyzések. 1. A P. 336. problémában adódik, hogy speciális háromszögünkben

C D F E

húrnégyszög.
2. Sokan trigonometriai eszközökkel bizonyították az állítást ‐ nagyon hosszan.