| Feladat: | F.2258 | Korcsoport: 18- | Nehézségi fok: nehéz |
| Megoldó(k): | Bohus G. , Csere K. , Csikós Zs. , Dósa Gy. , Elek G. , Feledi Gy. , Fodor L. , Hátsági Zs. , Heckenast L. , Horváth 718 I. , Kapos L. , Kappelmayer Hedvig , Károlyi Gy. , Kiss 352 Gy. , Kovács 134 I. , Maloveczky Gy. , Mészáros G. , Ódor T. , Simonyi G. , Somogyi H. , Sz. Nagy Cs. , Szegedy P. , Szenes A. , Vértesi L. | ||
| Füzet: | 1980/november, 128 - 130. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Terület, felszín, Gömb és részei, Szabályos tetraéder, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1980/április: F.2258 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Egyszerűbben írható le a feladat tárgya az alábbi észrevétel alapján. Az szabályos tetraéder magasságszakaszának felező merőleges síkja azonos az sík tükörképével a körülírt gömb középpontjára nézve. Valóban, szabályos tetraéderben azonos az súlyponttal. azonos az szabályos háromszöglap körülírt körének középpontjával. Így a szakasz tetraéderünknek egyben súlyvonala is, és rajta (egyben ) a -höz közelebbi negyedelőpont, tehát -nek ‐ ami az síkon van ‐ -ra való tükörképe felezi a magasságot. 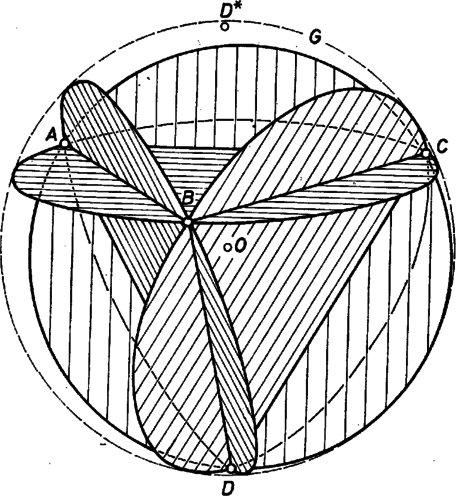 Könnyű ebből belátni, hogy a körülírt gömb felületén az előírt síkok által létrehozott részek szintén -ra való tükörképei azoknak a részeknek, amelyekre felületét az , , és lapsíkokkal kimetszett kiskörök feldarabolják. Elég tehát az utóbbi felosztás részeinek felszínével foglalkoznunk, illetve a mondott kétféle felületrész arányával. Az lapsík által kimetszett kör két gömbsüvegre vágja szét felületét. A -t tartalmazó süveg magassága , tehát a másiké , itt a -nek -vel átellenes pontja. Így a süvegek felszínei , illetve , ahol most a gömb felszínét jelöli, hiszen a gömbsüveg felszíne arányos a magasságával. (Nem származhat félreértés a jel kétféle jelentéseiből.) Az , , pontok 3 egyenlő ívre osztják -et. A többi 3 lapsík által kimetszett köröknek ívük esik a fenti kisebb gömbsüvegbe, az sík által kimetszett kör íve és között létesít új összeköttetést, a továbbiak és , illetve és között. Nincs közös pontjuk a kis gömbsüveg belsejében, hiszen mindegyiknek a teljes köre lent átmegy -n, és ezért legmagasabb pontjuk felé haladva távolodunk -tól. (Úgy tartjuk -t, hogy felső pontja .) Eszerint a kis gömbsüveg 4 részre van felosztva, ebből 3-at körív határol ‐ pl. egyet és két összekötése ‐, és ez a "kétcsúcsú rész'' egybevágó. A negyedik részt 3 körív határolja, ez a háromcsúcsú felületi rész. Ugyanígy mindegyik lapsík által lemetszett kisebbik gömbsüveg 3 kétcsúcsú és 1 háromcsúcsú felületi részre oszlik, pl. az sík által az , és kétcsúcsúak (az elsőt már másodszor látjuk) és az háromcsúcsú rész és az egyező típusú részek egybevágók. Ezek szerint a test mindegyik éléhez hozzárendelhető egy kétcsúcsú rész és mindegyik lapjához egy háromcsúcsú, tehát számuk egész felületén 6, illetve 4. Erről a kétféle részről szól a bizonyítandó állítás. Látjuk most már, hogy a által létrejött nagyobbik gömbsüveg (az alsó) ugyancsak 3 kétcsúcsúra, továbbá 3 háromcsúcsúra darabolódott fel. Így a többlete a kisebbikhez képest éppen 2 háromcsúcsúnak a felszínével egyenlő: Így a háromcsúcsúak együttes felszíne , és a hátra levő oszlik el a 6 kétcsúcsúra: , ami pedig ; éppen ezt kellett bizonyítanunk. |