Kezdőlap


Feladat:	F.2252	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Csikós Zs. , Szegedy P. , Zsilinszky L.
Füzet:	1980/október, 66 - 67. oldal		PDF \| MathML
Témakör(ök):	Aranymetszés, Szabályos testek, Feladat
Hivatkozás(ok):	Feladatok: 1980/március: F.2252

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a szabályos oktaéder középpontját $O$ -val, egy lapjának csúcsait $A, B, C$ betűvel, így a hátra levő 3 csúcs az utóbbiaknak $O$ -ra való $A', B', C'$ tükörképe. Legyen $P$ az $A B$ él kijelölt pontja úgy, hogy $P A : P B = 1 : (\sqrt[]{5} + 1) / 2$ ‐ röviden $1 : k$ , vagyis $k > 1$ ‐, tehát $P A$ az él kisebbik része, $P B$ a nagyobbik rész.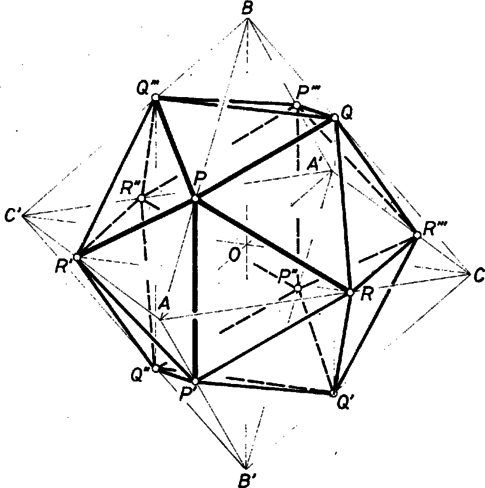
Alkalmazzuk a váltakozás követelményét egyelőre $A$ -ban és $B$ -ben a $C$ felé irányuló élek $R$ , ill. $Q$ osztópontjára, ez a két él $C$ -ből nézve szomszédos. És mivel $A$ és $B$ miatt $Q B$ -t kisebbnek, $R A$ -t a nagyobb résznek kell választanunk, ami által $C Q$ a nagyobb rész lesz, $C P$ pedig a kisebb, és ezek különbözők, nem jutottunk ellentmondásba a kiválasztás elvével.

Áttérve a szomszédos

A C B'

lapra, az

A B'

élen az

A

-hoz közelebbi

P'

osztópont kijelölése esedékes, az pedig éppen

P

tükörképe az oktaéder

O A C = S_{b}

szimmetriasíkjára, ahogyan az

A C B'

lap ugyanilyen képe az

A C B

lapnak. Hasonlóan a

C B'

élen

C

körüljárása szerint kijelölendő

Q'

pontra

Q' C > Q' B'

, tehát

Q'

Q

képe

S_{b}

-re. Így

A

és

C

körüljárásában immár 3‐3 élen teljesítettük a váltakozást.
Az

A C'

élen az

A

-tól távolabbi

R'

pontot választva,

A

körüljárása az előírás szerint záródik, hiszen

A

-ban 4 lap, 4 él fut össze, és a 4 páros szám.

R'

R

képe az

O A B = S_{c}

síkra. Hasonlóan a

B, C, B', C'

csúcsokban 3‐3 egymás utáni élre lesz helyes a körüljárás, ha

C' B'

-n és

C' B

-n a

Q'

-nek, ill.

Q

-nak

S_{c}

-re való

Q'', Q'''

képét választjuk. Végül az

A

körüli

P, R, P', R'

pontnégyesnek az

O B C = S_{a}

síkra való tükörképét véve, minden csúcs körül megfelel a kiválasztás, és ezzel beláttuk az a) állítás helyességét. ‐ Bizonyításunk egyrészt az oktaéder egyes szimmetriáin alapult, másrészt azon a tényen, hogy az oktaédercsúcsokból kifutó élek 4-es létszáma osztható a kiválasztási elvben előírt ismétlődés 2-es periódusával.

2. Az oktaéder további szimmetriái alapján adódik, hogy a kiválasztott 12 pont bármelyike átvihető bármelyik másikba úgy, hogy egyidejűen minden egyes kijelölt pont kijelölt pontba jusson. Valóban: bármelyik oktaédercsúcs átvihető bármelyik másikba (a mondott további követelménnyel, többféleképpen is), és ha egyidejűen pontegyüttesünk nem önmagába ment át, akkor egy

90^{\circ}

-os elfordítás eredményezi ezt. ‐ Eszerint pontjaink egy

O

körüli gömbön vannak rajta.
Megmutatjuk, hogy

P

-től 5 másik kiválasztott pont van egyenlő távolságra, ahogy a szabályos ikozaéder minden csúcsával 5 másik csúcs szomszédos, és együtt 5 szabályos háromszöget alkotnak. A

P Q R

háromszög nyilvánvalóan szabályos, és hosszegységnek választva

A P

-t, oldalára a cosinustétel szerint

\begin{matrix} P Q = \sqrt[]{l + k^{2} - k} = \sqrt[]{2} = P R . \end{matrix}

Ugyanekkora az

A B C'

háromszögből

P Q'''

és

P R'

is, továbbá

P P'

is, hiszen az

A B A' B'

metszet négyzet, és így

A P P'

egyenlő szárú derékszögű háromszög, egységnyi befogókkal.
Ezek szerint

P', R, Q, Q'''

és

R'

egy a

P

körüli gömbön is rajta vannak. Két (nem koncentrikus) gömb közös pontjai ‐ ha vannak ‐ egy körön vannak, vagyis egy síkban, eszerint

P' R Q Q''' R'

síkbeli ötszög. Másrészt oldalai is egyenlőek a fentiek szerint, tehát

P O

mint tengely körüli

72^{\circ}

-os elfordításokkal az ötszög csúcsai ciklikusan egymásba mennek át.
Ugyanez a pontegyüttes bármelyik pontjára is érvényes. Jelöljük a háromszöglapok számát

h

-val, és építsük össze a test modelljét csupa különálló szabályos háromszögből. A

h

db lapon eredetileg

3 h

csúcs van, az 5-ösével való összeragasztás után

3 h / 5

, és ez egyenlő 12-vel, kijelölt pontjaink létszámával; innen

h = 20

, tehát a test valóban szabályos ikozaéder. ‐ A meghatározást úgy értettük, hogy a 12 pont együttesének konvex burka az ikozaéder.