Kezdőlap


Feladat:	F.2244	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Balla 222 L. , Barla F. , Beleznay F. , Bohus G. , Bölcsföldi L. , Csikós Zs. , Czakó F. , Elek G. , Elter J. , Feledi Gy. , Gerencsér Gy. , Halász P. , Heckenast L. , Horváth 718 I. , Kámán L. , Kántor Zs. , Kapos L. , Kappelmayer Hedvig , Károlyi Gy. , Kelemen B. , Kiss 352 Gy. , Kiss E. , Kovács 134 I. , Kurusa Á. , Megyeri L. , Mihálykó Cs. , Ódor T. , Regős Enikő , Simonyi G. , Sz. Nagy Cs. , Szakony L. , Szegedy P. , Szirmay L. , Umann G. , Weisz F. , Zsilinszky L. , Öreg E. Zs.
Füzet:	1980/november, 120 - 121. oldal		PDF \| MathML
Témakör(ök):	Háromszögek nevezetes tételei, Szögfelező egyenes, Beírt kör, Síkgeometriai számítások trigonometria nélkül háromszögekben, Feladat
Hivatkozás(ok):	Feladatok: 1980/február: F.2244

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a beírt kör érintési pontja a $B C$ , $B A$ oldalon $A_{1}$ , illetve $C_{1}$ , a $B C$ , $A C$ oldalszakasz felezőpontja $A_{0}$ , illetve $B_{0}$ , továbbá az $A_{1} C_{1}$ és $A_{0} B_{0}$ egyenesek metszéspontja $N$ . Azt mutatjuk meg a feladat állításának bizonyításául, hogy az $A N$ egyenes azonos az $A$ -beli belső szögfelezővel.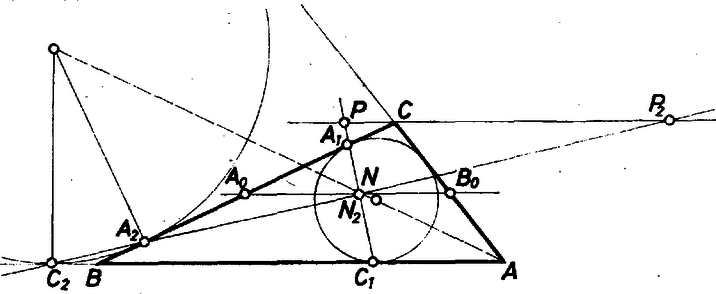

1. ábra

Messe

A_{1} C_{1}

C

-n átmenő,

A B

-vel párhuzamos egyenest

P

-ben (1. ábra). Ekkor egyrészt a

P C A_{1}

és

C_{1} B A_{1}

háromszögek centrálisan hasonlók az

A_{1}

centrumra, mert

A_{1}

-en megy át 2‐2 oldalegyenesük, a harmadik pár pedig párhuzamos. Ebből

A_{1} B = C_{1} B

alapján, felhasználva az érintőszakaszra ismert kifejezést:

\begin{matrix} P C = A_{1} C = s - A B, (2 s = A B + B C + C A) . \end{matrix}

Másrészt a

P C A C_{1}

négyszög trapéz, és ebben a középvonalra

\begin{matrix} N B_{0} = \frac{1}{2} (A C_{1} + P C) = \frac{(s - B C) + (s - A B)}{2} = \frac{A C}{2} = A B_{0} . \end{matrix}

Eszerint az

N A B_{0}

háromszög egyenlő szárú, tehát

\begin{matrix} C A N ∢ = B_{0} A N ∢ = B_{0} N A ∢ = B A N ∢, \end{matrix}

ezt akartuk bizonyítani.

2. Vegyük a beírt kör helyére először a

B C

oldalhoz kívülről hozzáírt kört, vagyis amelyik az

A B

és

A C

félegyeneseket érinti, éspedig

A B

-t

C_{2}

-ben ‐ ahol, mint ismeretes,

A C_{2} = s

‐, a

B C

oldalt pedig

A_{2}

-ben. Az ábra szerint az

A_{2} C_{2}

egyenes szintén átmegy az előbbi

N

ponton, tehát a feladat állítása érvényes, ha

A_{1} C_{1}

helyére

A_{2} C_{2}

-t vesszük.
Valóban,

P

helyére véve a

P C

egyenesből az

A_{2} C_{2}

által kimetszett

P_{2}

pontot, a

P_{2} C A_{2}

és

C_{2} B A_{2}

hasonló helyzetű háromszögek

A_{2}

-re mint centrumra, egyenlő szárúak, így

P_{2} C = C A_{2} = C B - B A_{2} = C B - B C_{2} = C B - (s - A B) = s - A C

. Másrészt a

C_{2} A_{2}

, azaz

C_{2} P_{2}

egyenes szétválasztja az

A

C

csúcsokat, így

P_{2} C A C_{2}

hurkolt trapéz,

P_{2} C_{2}

szárának felezőpontját

N_{2}

-vel jelölve, középvonalára, vagyis a szárak felezőpontjai közti irányított távolságra

\begin{matrix} N_{2} B_{0} = \frac{1}{2} (A C_{2} - P_{2} C) = \frac{s}{2} - \frac{1}{2} (s - A C) = \frac{A C}{2} = N B_{0}, \end{matrix}

ezzel igazoltuk meglátásunk helyességét.

3. Hasonlóan lehet belátni, hogy az

A B

és az

A C

oldalhoz hozzáírt körök értelemszerűen veendő

A_{3} C_{3}

, illetve

A_{4} C_{4}

szelői ugyanabban az

N

pontban metszik az

A_{0} B_{0}

egyenest, és hogy az

N A

egyenes azonos az

A B C

háromszög

A

-nál levő külső szögeinek közös felező egyenesével (ez a két szög egymásnak csúcsszöge, 2. ábra).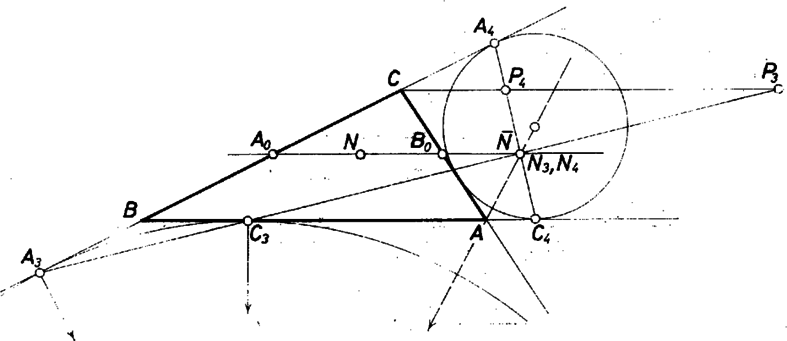

2. ábra

Mindezek szerint kimondhatjuk:

kiválasztva egyrészt bármelyiket az

A B C

háromszög mindhárom oldalegyenesét érintő 4 kör közül, véve rajta a

B A

és

B C

egyenesekkel való érintési pontot, majd e két pont összekötő egyenesét,
véve másrészt a háromszög

B A

oldalával párhuzamos középvonalának egyenesét,
e két egyenes metszéspontját az

A

csúccsal összekötő egyenes átmegy a választott kör középpontján.

Megjegyzés. Számos megoldó trigonometriai vagy koordináta‐geometriai elemeket használt fel a bizonyításban.