Kezdőlap


Feladat:	F.2236	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bali J. , Beleznay F. , Benedek Ágnes , Biczó Anikó , Bohus G. , Bölcsföldi L. , Csere K. , Csikós Zs. , Feledi Gy. , Fodor L. , Halász P. , Heckenast L. , Horányi T. , Horváth 718 I. , Kappelmayer Hedvig , Kelemen B. , Király Z. , Kiss 352 Gy. , Kiss E. , Mendrey Zs. , Sz. Nagy Cs. , Szakál A. , Szegedy P. , Tóth V. , Umann G. , Weisz F. , Zsilinszky L.
Füzet:	1980/szeptember, 9 - 10. oldal		PDF \| MathML
Témakör(ök):	Másodfokú (és arra visszavezethető) egyenlőtlenségek, Paraméteres egyenlőtlenségek, Műveletek helyvektorok koordinátáival, Ellipszis egyenlete, Feladat
Hivatkozás(ok):	Feladatok: 1980/január: F.2236

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az $A = x - m$ , $B = y - n$ helyettesítéssel az (1) bal oldalán álló kifejezésből $(A^{2} + A B + B^{2})$ -t kapunk. Mivel ebben $A^{2}$ , $B^{2}$ együtthatója egyenlő, alkalmas $λ$ , $μ$ együtthatók mellett $[λ {(A + B)}^{2} + μ {(A - B)}^{2}]$ alakra hozható. Az együtthatók összehasonlításából kapjuk, hogy ekkor

\begin{matrix} λ + μ = 1, λ - μ = 1 / 2, \end{matrix}

vagyis

λ = 3 / 4

μ = 1 / 4

. Ezek alapján (1) ekvivalens a

\begin{matrix} {(3 \frac{x + y}{2} - 3 \frac{m + n}{2})}^{2} + \sqrt[]{3} {(3 \frac{x - y}{2} - \sqrt[]{3} \frac{m - n}{2})}^{2} ≦ 1 \end{matrix}

(2)

egyenlőtlenséggel, a mondott állítás pedig azzal, hogy tetszőleges

\begin{matrix} u = 3 \frac{x + y}{2}, v = \sqrt[]{3} \frac{x - y}{2} \end{matrix}

(3)

valós számpárhoz találhatók olyan

m

és

n

egészek, hogy a koordináta‐rendszer

P (u; v)

pontjának a

Q (a; b)

ponttól mért távolsága legfeljebb

1

, ahol

\begin{matrix} a = 3 \frac{m + n}{2}, b = \sqrt[]{3} \frac{m - n}{2} . \end{matrix}

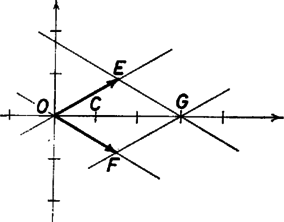
A koordináta‐rendszerben az origóból a

Q

-ba mutató vektor

(m e + n f)

alakú, ahol

e

és

f

az origóból az

\begin{matrix} E (\frac{3}{2}; \frac{\sqrt[]{3}}{2}), F (\frac{3}{2}; - \frac{\sqrt[]{3}}{2}) pontokba mutató vektor. \end{matrix}

Könnyen látható, hogy az

E

F

pontok az

O

origóval együtt egy szabályos háromszög csúcsait adják, amelynek centruma a

C (1; 0)

pont.
Ha

n = 0

, a különböző

m

-ekhez tartozó

Q

pontok az

O E

egyenesen sorakoznak, ha pedig

m = 0

Q

O F

egyenesen van. Általában pedig

Q

O E G F

paralelogrammából felépíthető rács valamelyik pontja, ahol

G

(3; 0)

pont. Mivel ez az

E F

átlója mentén két szabályos háromszögre vágható szét, azt is mondhatjuk, hogy az

O E F

háromszöggel egybevágó lemezekkel fedjük le a síkot hézagtalanul és átfedés nélkül. A feladat pedig azt kérdezi, hogy a sík tetszőleges pontjában található-e olyan háromszög-csúcs, amelyiktől a pont legfeljebb egységnyi távolságra van. Mivel az

O

E

F

pontok körüli egységsugarú körök mind átmennek az

O E F

háromszög

C

centrumán, ezek együtt lefedik a háromszöget. Így a feladat kérdésére igen a helyes válasz.

Megjegyzések. A megoldás kulcsa a (3) alatti helyettesítés: ez viszi a (2) feltételnek eleget tevő tartományt körbe. Mivel a (3)-hoz hasonló ún. lineáris helyettesítések kört mindig ellipszisbe visznek, ez azt jelenti, hogy az

\begin{matrix} x^{2} + x y + y^{2} ≦ 1 / 3 \end{matrix}

(4)

feltételnek eleget tevő pontok egy ellipszis-lemez pontjai. A feladat kérdése azt jelenti, hogy a különböző

(m, n)

centrumokhoz tartozó (4) alatti ellipszisek együtt lefedik-e a síkot. Beláthattuk volna ezt úgy is, hogy először megmutatjuk, hogy az

\begin{matrix} (\frac{1}{3}; \frac{1}{3}), (- \frac{1}{3}; \frac{2}{3}), (- \frac{2}{3}; \frac{1}{3}), \\ (- \frac{1}{3}; - \frac{1}{3}), (\frac{1}{3}; - \frac{2}{3}), (\frac{2}{3}; - \frac{1}{3}) \end{matrix}

pontok

m = n = 0

mellett benne vannak az (1) alatti tartományban, sőt az általuk meghatározott hatszög is e tartomány része, majd belátjuk, hogy ha e hatszög centrumát az

(x; y)

sík tetszőleges

(m; n)

pontjába áthelyezzük, a kapott hatszögek együtt lefedik a síkot.
2. Belátható, hogy a

\begin{matrix} c_{0} x^{2} + c_{1} x y + c_{2} y^{2} ≦ c \end{matrix}

feltételnek eleget tevő pontok akkor és csak akkor alkotnak egy ellipszislemezt, ha

c_{0}

és

c_{2}

pozitív, valamint

4 c_{0} c_{2} > c_{1}^{2}

. Az ezzel egybevágó, különböző

(m, n)

centrumú ellipszisek akkor és csak akkor fedik a síkot, ha még

\begin{matrix} c ≧ \frac{c_{0} c_{2}}{4 c_{0} c_{2} - c_{1}^{2}} (c_{0} + c_{2} - | c_{1} |) \end{matrix}

(5)

is teljesül. Így ha a

c

szám eleget tesz az (5) feltételnek, akkor minden

(x, y)

valós számpárhoz található olyan

m

és

n

egész, amelyikre

\begin{matrix} c_{0} {(x - m)}^{2} + c_{1} (x - m) (y - n) + c_{2} {(y - n)}^{2} ≦ c \end{matrix}

igaz.