Kezdőlap


Feladat:	F.2226	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	1980/március, 113 - 115. oldal		PDF \| MathML
Témakör(ök):	Derékszögű háromszögek geometriája, Természetes számok, Pitagoraszi számhármasok, Feladat
Hivatkozás(ok):	Feladatok: 1979/november: F.2226

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a $B C D$ háromszög $C$ -nél levő szöge $90^{\circ}$ -os, és a $B$ -nél, $D$ -nél levő szögek közül a $B$ -nél levő legyen a kisebb. A $B C$ egyenes $B D$ -re vonatkozó tükörképe messe $C D$ -t $A$ -ban, és az $A B$ , $B C$ , $C A$ , $C D$ , $D A$ szakaszok hosszát jelöljük rendre $c$ -vel, $a$ -val, $b$ -vel, $d$ -vel, $e$ -vel. Mivel az $A B C$ háromszögben $B D$ szögfelező, $a : c = d : e$ , továbbá Pitagorasz tétele szerint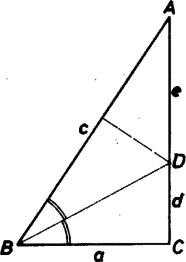

\begin{matrix} c^{2} = a^{2} + {(d + e)}^{2} . \end{matrix}

Írjunk itt

e

helyére

c d / a

-t, és fejezzük ki a kapott összefüggésből

c

-t, majd

b

-t:

\begin{matrix} c = \frac{a^{2} + d^{2}}{a^{2} - d^{2}} a, b = \frac{2 a^{2} d}{a^{2} - d^{2}} \end{matrix}

c

-re adódó másodfokú egyenlet másik gyöke negatív).

Ha most a kapott

A B C

háromszög oldalait

(a^{2} - d^{2}) / a

-szorosukra nyújtjuk, az új

A' B' C'

háromszög oldalainak a hossza rendre

\begin{matrix} a' = a^{2} - d^{2}, b' = 2 a d, c' = a^{2} + d^{2} \end{matrix}

(1)

lesz. Ennek alapján elegendő olyan

B C D

háromszöget találnunk, melyben

a

és

d

egészek, továbbá a

C B D

szög nagyobb

ε / 2

-nél.

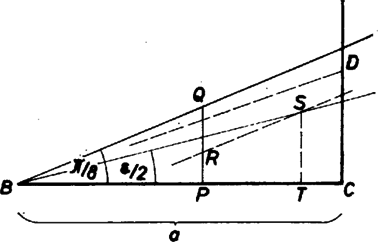Mérjük fel egy tetszőleges

B P

félegyenesre az

ε / 2

π / 8

szögeket, és messe az utóbbi szárát a

B P

-re

P

-ben emelt merőleges

Q

-ban. Mérjük fel a

Q

-ból

P

felé induló félegyenesre az egységnyi hosszú

Q R

szakaszt, és húzzunk párhuzamost

R

-en át

B Q

-val. Ez valahol metszi az

ε / 2

szög szárát, jelöljük ezt a pontot

S

-sel,

S

-nek

B P

-n levő vetületét

T

-vel. Legyen

C

B P

félegyenes tetszőleges,

T

-n túli pontja, melyre

a = B C

egész szám. A

C

-ben

B P

-re emelt merőlegesnek az

ε / 2

π / 8

szögek szárai közti darabja hosszabb az egységül választott

Q R

szakasznál, így biztosan van benne olyan

D

pont, amelyre

C D

egész. (Ha a

B P

-re

C

-ben emelt merőlegesre egymás után egységnyi hosszúságú szakaszokat mérünk fel, ezek végpontjainak a sorozata nem ugorhatja át ezt a szakaszt.) Készen vagyunk, megvan az a

B C D

háromszög, amit kerestünk, a feladat állítását ezzel beláttuk.

Megjegyzések. 1. Akik csak képletekben hajlandók gondolkodni, most azt mondják: igen, tudni kellett a pitagoraszi számhármasokat. Valóban

(1)

ezek jól ismert képlete. Ne tévesszük azonban szem elől, hogy
‐ a pitagoraszi számhármasok előállításának a nem-triviális fele az, hogy minden derékszögű háromszöghöz van olyan

a

és

d

egész, hogy

(1)

előállítja a háromszög

a'

b'

c'

oldalait, ha

a'

b'

c'

egészek [az, hogy

(1)

derékszögű háromszöget ad meg, nyilvánvaló];
‐ nekünk ehelyett arra volt szükségünk, hogy uralni tudjuk a kapott háromszög szögeit

a

d

alkalmas megválasztásával, ami a pitagoraszi hármasok levezetésénél nem szokott szerepelni.

2. Belátható a feladat állítása annak alapján is, hogy megmutatjuk, tetszőleges

n

természetes számhoz található olyan nála nagyobb

a

természetes szám, hogy az

a

(a + 1)

befogókkal rajzolt derékszögű háromszög átfogójának a hossza egész szám. Más szóval azt mutatjuk meg, hogy a

\begin{matrix} 2 c^{2} - {(2 a + 1)}^{2} = 1 \end{matrix}

(2)

egyenlet egész gyökpárjai között tetszőlegesen nagy található. Ilyen egyenletekről sokszor volt már szó lapunkban (általános megoldásukról Fried Ervin írt cikksorozatot), így az is többször szerepelt már, hogyan lehet

(2)

egyetlen gyökpárjából végtelen sokat előállitani.