Kezdőlap


Feladat:	F.2220	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	1980/február, 63 - 66. oldal		PDF \| MathML
Témakör(ök):	Trigonometriai azonosságok, Derékszögű háromszögek geometriája, Beírt kör, Hozzáírt körök, Mértani sorozat, Feladat
Hivatkozás(ok):	Feladatok: 1979/október: F.2220

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ismert, hogy a háromszög $t$ területére, beírt és hozzáírt köreinek $ϱ$ , $ϱ_{a}$ , $ϱ_{b}$ és $ϱ_{c}$ sugaraira, valamint $s$ félkerületére érvényesek a következő összefüggések:

\begin{matrix} t = ϱ \cdot s = ϱ_{a} (s - a) = ϱ_{b} (s - b) = ϱ_{c} (s - c) . \end{matrix}

Feladatunkban ‐ mivel nyilván a beírt kör a legkisebb és bármelyik két sugár hossza különböző ‐ föltehetjük, hogy az oldalak nagyságviszonya:

a < b < c

. Ezért

\begin{matrix} ϱ_{a} = q \cdot ϱ, ϱ_{b} = q^{2} \cdot ϱ, ϱ_{c} = q^{3} \cdot ϱ, \end{matrix}

ahol

q

a mértani sorozat hányadosa

(q > 1)

.
Ezek szerint

\begin{matrix} q = \frac{ϱ_{a}}{ϱ} = \frac{ϱ_{c}}{ϱ_{b}}, azaz \frac{s}{s - a} = \frac{s - b}{s - c}, & (1) \\ s (s - c) = (s - b) (s - a), \\ (a + b + c) (a + b - c) = (c + a - b) (c - (a - b)), \\ {(a + b)}^{2} - c^{2} = c^{2} - {(a - b)}^{2}, \\ a^{2} + b^{2} = c^{2}, \end{matrix}

tehát Pitagorasz tételének megfordítása szerint a háromszög csak derékszögű lehet ‐ ha egyáltalán létezik ‐, más szóval legnagyobbik szöge csak

γ = 90^{\circ}

lehet.
Mivel azonban ennek megállapításában (1)-ben csak két arányt használtunk fel, azt még nem tudjuk, van-e olyan derékszögű háromszög, amelyben a

\begin{matrix} \frac{ϱ_{b}}{ϱ_{a}} = q \end{matrix}

követelmény is teljesül. Ennek tisztázására a verseny ideje nem lett volna elegendő (lásd az alábbi 3. megjegyzést).

Megjegyzések. 1. Néhányan még ismerik az itt következő képleteket, amelyek alapján numerikus példában ,,kényelmesebben'' (azaz logaritmustáblázattal) számíthatók a szögek az oldalakból, mint a ,,nehézkes'' cosinustétellel:

\begin{matrix} tg \frac{γ}{2} = \sqrt[]{\frac{(s - a) (s - b)}{s (s - c)}}, sin \frac{γ}{2} = \sqrt[]{\frac{(s - a) (s - b)}{a b}}, cos \frac{γ}{2} = \sqrt[]{\frac{s (s - c)}{a b}} . \end{matrix}

(A további két szögre vonatkozó hasonló képletek természetesen az oldalak ciklikus permutációjával írhatók föl, ami közben persze

s

változatlan marad.)
Az első képlet alapján közvetlenül

\begin{matrix} tg \frac{γ}{2} = \sqrt[]{\frac{ϱ \cdot ϱ_{c}}{ϱ_{a} \cdot ϱ_{c}}} = \sqrt[]{\frac{ϱ^{2} q^{3}}{ϱ^{2} q^{3}}} = 1, \end{matrix}

\frac{γ}{2} = 45^{\circ}

γ = 90^{\circ}

. Itt a háromszög létezése biztos, mert a képletek csak nemlétező háromszögek esetére adnak értelmetlen eredményt.

2. Az említett képletek ‐ és több hasonló is ‐ a matematikának ‐ pontosabban a számítások végrehajtása technikájának ‐ abból a korszakából valók, amikor a végrehajtás legfejlettebb eszköze a logaritmustáblázat volt. Arra a korszakra következtek ‐ csak nagy ugrásokban nézve ‐ a fogaskerekekkel működő asztali számológépek, előbb kézi, majd motoros működtetéssel, ma pedig az elektronikus kalkulátorok. (A logarlécet kihagytuk, ez amazok mellett csak gyors becslésekre való.) ‐ A képletek persze ma is érvényesek. ‐ Szerepel azonban a

tg x / 2

pl. bizonyos integrálok transzformálásában is; de felsorolni sem lehet az ilyenféle, az elméletben is jól felhasználható apró fogásokat.

3. A

ϱ_{b} : ϱ_{a} = q

követelményt is teljesítő derékszögű háromszög nagyobbik hegyes szöge felének tangensére harmadfokú egyenletet kapunk. A föntebbihez hasonlóan

\begin{matrix} tg \frac{β}{2} = \sqrt[]{\frac{(s - a) (s - c)}{s (s - b)}} = \sqrt[]{\frac{ϱ \cdot ϱ_{b}}{ϱ_{a} \cdot ϱ_{c}}} = \frac{1}{q} és \\ tg \frac{α}{2} = \frac{1}{q^{2}} \end{matrix}

(vagyis a félszögek tangensei is mértani sorozatot alkotnak,

3

elemmel, ugyanazzal a hányadossal). Ezek alapján

\begin{matrix} {tg}^{2} \frac{β}{2} = \frac{1}{q^{2}} = tg \frac{α}{2} = tg (45^{\circ} - \frac{β}{2}) = \\ = \frac{1 - tg \frac{β}{2}}{1 + tg \frac{β}{2}} = \frac{1 - \frac{1}{q}}{1 + \frac{1}{q}} = \frac{q - 1}{q + 1}, \\ q^{3} - q^{2} - q - 1 = 0. \end{matrix}

(Ez a ,,szép'' egyenlet számos más, egyszerűen megfogalmazható probléma megoldásában is fel-felbukkan.) Közelítő megoldása:

\begin{matrix} q = 1, 83929, α = 32^{\circ} 56' 6'', β = 57^{\circ} 3' 54'' . \end{matrix}

II. megoldás. Az előző megoldás jelölésein túl legyenek a háromszög csúcsai

A

B

C

, a beírt kör középpontja

O

, a hozzáírt köröké rendre

O_{a}

O_{b}

O_{c}

úgy, hogy az

O_{a}

középpontú kör az

A B

A C

oldalak meghosszabbításait érinti, valamint a

B C

oldalt kívülről, és így tovább. Így az

O O_{a}

egyenes a

B A C

szöget felezi, az

O_{b} O_{c}

pedig az

A

-nál levő külső szögeket, tehát merőleges

O A

-ra.

O

O_{a} O_{b} O_{c}

háromszögre nézve magasságpont, és belső pontja a háromszögnek, tehát ez a háromszög hegyesszögű.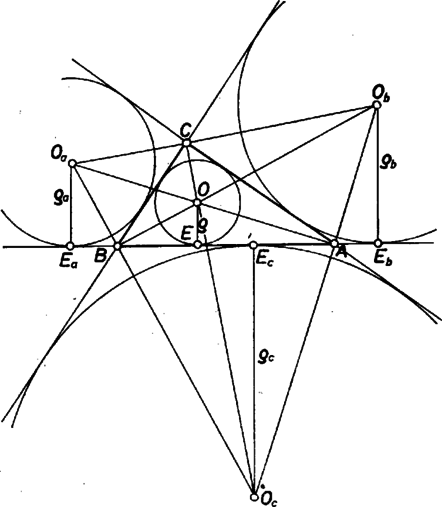

Jelöljük a körök érintési pontját az

A B

egyenesen rendre

E

E_{a}

E_{b}

E_{c}

-vel. Így az

A O E

és

A O_{a} E_{a}

, valamint az

A O_{b} E_{b}

és

A O_{c} E_{c}

hasonló derékszögű háromszög-párokból

\begin{matrix} \frac{A O_{a}}{A O} = \frac{E_{a} O_{a}}{E O} = \frac{ϱ_{a}}{ϱ} = q = \frac{ϱ_{c}}{ϱ_{b}} = \frac{E_{c} O_{c}}{E_{b} O_{b}} = \frac{A O_{c}}{A O_{b}} . \end{matrix}

q

-tól jobbra látható elemek logikai sorrendje jobbról balfelé olvasva ugyanaz, mint a többieké balról

q

-ig.) Végezzünk kis cserét a sor két végén álló arányokban:

\begin{matrix} \frac{A O_{a}}{A O_{c}} = \frac{A O}{A O_{b}}, \end{matrix}

eszerint az

A O_{a} O_{c}

és

A O O_{b}

derékszögű háromszögek befogóinak aránya egyenlő. Ezért ez a két háromszög hasonló. Egy-egy megfelelő szögükre és az utóbbinak a csúcsszögére

\begin{matrix} A O_{a} O_{c} ∢ (= O O_{a} B ∢) = A O O_{b} ∢ = O_{a} O B ∢, \end{matrix}

ez pedig azt jelenti, hogy a

B

-nél derékszögű

O O_{a} B

háromszög hegyesszögei egyenlők, tehát mindegyik

45^{\circ}

.
Másfelől az

O O_{a}

szakasz fölötti Thalész-kör átmegy

B

-n és

C

-n, és ezek

O O_{a}

-nak átellenes oldalán vannak, ezért

\begin{matrix} \frac{A C B ∢}{2} = O C B ∢ = O O_{a} B ∢ = 45^{\circ}, \end{matrix}

tehát

A C B ∢ = 90^{\circ}

, akkor pedig ez az

A B C

háromszög legnagyobb szöge. Ezzel megkaptuk a választ a feladat kérdésére.