Kezdőlap


Feladat:	F.2216	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bohus Géza , Szegedy P.
Füzet:	1980/január, 15 - 16. oldal		PDF \| MathML
Témakör(ök):	Tengelyes tükrözés, Szögfelező egyenes, Síkbeli ponthalmazok távolsága, Síkgeometriai számítások trigonometria nélkül háromszögekben, Feladat
Hivatkozás(ok):	Feladatok: 1979/szeptember: F.2216

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Mozgassunk egy $P$ pontot a $D E$ egyenesen, jellemezzük helyzetét a $D P = x$ előjeles szakasszal, amit $E$ felé vegyünk pozitívnak. $P$ -nek az $A B = e_{3}$ egyenestől való távolsága mint $x$ függvénye

\begin{matrix} d_{3} (x) = d_{3} (0) + x sin φ, \end{matrix}

(1)

ahol

φ

D E

és

B A

egyenesek szöge, és

d_{3} (0)

természetesen

D

-nek

A B

fölötti magassága. Könnyű belátni, hogy

d_{3} (D E) ⋚ d_{3} (0)

aszerint, hogy

C A ⋚ C B

, és ha ezek nem egyenlők, akkor elég nagy abszolút értékű

x ≶ 0

mellett

d_{3} (x)

negatívnak adódik, mert

P

átlép

e_{3}

-on, ennek

C

-t és a háromszöget nem tartalmazó partjára. Ilyenkor feladatunkban természetesen

| d_{3} (x) |

-ét használjuk majd föl.

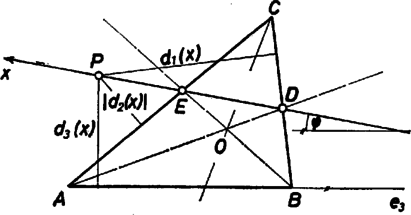Válasszuk

D E

-t hosszegységnek, ekkor

E

-re

x = 1

, és kiküszöbölhetjük (1)-ből a szöget:

d_{3} (1) = d_{3} (0) + sin φ

, tehát

\begin{matrix} d_{3} (x) = d_{3} (0) + x (d_{3} (1) - d_{3} (0)) . \end{matrix}

(2)

Látjuk, hogy

d_{3} (x)

x

-nek elsőfokú függvénye. Nyilván ugyanez áll

P

-nek

B C

-től,

C A

-tól mért, ugyanígy értelmezett

d_{1} (x)

, illetve

d_{2} (x)

távolságára. Ezekre

D

-ből

d_{3} (0) = d_{2} (0)

és

E

révén

d_{3} (1) = d_{1} (1)

‐ itt használtuk föl

D

és

E

szögfelezős származtatását ‐, továbbá

d_{1} (0) = 0

és

d_{2} (1) = 0

, mert

D, E

rajta van

B C

-n, illetve

A C

-n.
Így

d_{1} (x)

-nek és

d_{2} (x)

-nek 2 ‐ 2 helyen fölvett értékét ismertként kezelhetjük, és (2)-höz hasonlóan

\begin{matrix} d_{1} (x) = d_{1} (0) + x (d_{1} (1) - d (0)), azaz \\ d_{1} (x) = x \cdot d_{1} (1), \end{matrix}

és ugyanígy

\begin{matrix} d_{2} (x) = d_{2} (0) - x \cdot d_{2} (0) . \end{matrix}

Ezekből ‐ az említett egyenlőségeket is fölhasználva ‐ minden

x

-re:

\begin{matrix} d_{1} (x) + d_{2} (x) = d_{2} (0) + x (d_{1} (1) - d_{2} (0)) = d_{3} (0) + x (d_{3} (1) - d_{3} (0)) = d_{3} (x), \end{matrix}

(3)

és ez tüstént az állítás igazolása

P

-nek minden olyan helyzetére, amelyre egyik

d_{i} (x)

sem negatív

(i = 1,2,3)

, és közülük

d_{3} (x)

a legnagyobb. Van ilyen helyzete

P

-nek, a

D E

szakasz minden pontja ilyen, más szóval: amikor

P

C

-t tartalmazó

D O E

szögtartományban halad, beleértve az

O D

O E

félegyeneseket. Ugyanis ekkor

P

a háromszög belsejében van (illetve a kerületén), továbbá a síknak az

A D

szögfelezővel való kettévágása révén

d_{3} (x) ≧ d_{2} (x)

, és

B E

révén

d_{3} (x) \geq d_{1} (x)

.
Amint

P

átlép

E

-n, egyrészt

d_{2} (x)

negatív lesz, mert átlépte az

A C

oldalegyenest, másrészt

d_{1} (x)

nagyobb lesz, mint

d_{3} (x)

, mert a

B E

szögfelezőt is átlépte; továbbá

d_{1} (x) > | d_{2} (x) |

is teljesül, mert ez a nagyságviszony a

C O

szögfelezőn átlépve fordul az ellentétesre, ezt pedig

P

már

D

és

E

közt átlépte. Ezek szerint

d_{1} (x)

a három távolság legnagyobbika,

d_{2} (x) = - | d_{2} (x) |

és (3)-ból

d_{1} (x) = d_{3} (x) + | d_{2} (x) |

, tehát az állítás ekkor is érvényes.
A legutóbbiakból úgy kapjuk az állítást a

D E

szakasz

D

-n túli meghosszabbításán levő

P

pontokra, hogy az 1-es és 2-es indexeket fölcseréljük egymással.

Bohus Géza (Budapest, Fazekas M. Gyak. Gimn., IV. o. t.)

Megjegyzés.

C A = C B

esetén az állítás elemi tükrözésekkel is könnyen belátható.