Kezdőlap


Feladat:	F.2215	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bánkúti Gyöngyi , Beleznay F. , Bölcsföldi L. , Csikós Zs. , Dénes L. , Elek G. , Guba L. , Heckenast L. , Kámán L. , Károlyi Gy. , Kiss 352 Gy. , Kiss E. , Kovács 134 I. , Krähling János , Lévai P. , Lipusz Cs. , Nagy Kolozsvári Á. , Osváth Z. , Szabó 457 L. , Szegedy P. , Szirmay L. , Tarcsay M. , Várkonyi B.
Füzet:	1980/január, 13 - 15. oldal		PDF \| MathML
Témakör(ök):	Téglatest, Szélsőérték-feladatok differenciálszámítás nélkül, Vektorok skaláris szorzata, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1979/szeptember: F.2215

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. 1. Legyen $E$ egy pont $e$ -nek a testbeli szakaszán, és jelöljük az $E D A$ , $E D B$ , $E D C$ szögeket sorra $α$ , $β$ , $γ$ betűvel; ezekre nyilvánvalóan $0^{\circ} < α$ , $β$ , $γ < 90^{\circ}$ . A kérdéses távolságösszeg:

\begin{matrix} s = a sin α + b sin β + c sin γ . \end{matrix}

(1)

Válasszuk

D E

-t hosszegységnek, így vetületei a

D

-ből kifutó éleken rendre

cos α

cos β

cos γ

, és az ezek végpontjaival meghatározott téglatest testátlójaként

\begin{matrix} {D E}^{2} = 1 = {cos}^{2} α + {cos}^{2} β + {cos}^{2} γ = (1 - {sin}^{2} α) + (2 - {sin}^{2} β - {sin}^{2} γ), \end{matrix}

amiből minden szóba jövő

α, β, γ

szöghármasra

\begin{matrix} {sin}^{2} α + {sin}^{2} β + {sin}^{2} γ = 2. \end{matrix}

(2)

Írjuk a bal oldalt a bizonyítandó egyenlőtlenség

2

-es tényezője helyére:

\begin{matrix} a sin α + b sin β + c sin γ ≦ \sqrt[]{(a^{2} + b^{2} + c^{2}) ({sin}^{2} α + {sin}^{2} β + {sin}^{2} γ)} . \end{matrix}

A bal oldal pozitív, így az állítás ekvivalens azzal az egyenlőtlenséggel, amit négyzetre emeléssel kapunk; abban mindent a jobb oldalra gyűjtünk, és észrevesszük a lehetőségeket a teljes négyzetté alakításra:

\begin{matrix} 0 ≦ {(a sin β - b sin α)}^{2} + {(b sin γ - c sin β)}^{2} + {(c sin α - a sin γ)}^{2} . \end{matrix}

Ennek helyessége pedig nyilvánvaló.
2. Egyenlőségről csak akkor lehet szó, ha a jobb oldalon mindegyik zárójelben

0

áll; tovább ennek egzisztenciáját vizsgáljuk, a test éleire az

a ≦ b ≦ c

nagyságviszonyt alapul véve. A zárójelekbeli különbségek eltűnéséből:

\begin{matrix} \frac{sin α}{a} = \frac{sin β}{b} = \frac{sin γ}{c} = λ, állandó (> 0), \end{matrix}

tehát ha az adott téglatesthez van olyan

e

egyenes, amelyre

s

eléri felső korlátját, arra

α ≦ β ≦ γ

, elég tehát azt biztosítanunk, hogy

sin γ < 1

legyen.

λ

meghatározása céljára írjuk be (2)-be a

sin γ = λ c, ...

kifejezéseket, és vegyük észre, hogy az állításban is szereplő

(a^{2} + b^{2} + c^{2})

kifejezés téglánk

d

testátlójának négyzete. Így

λ = \sqrt[]{2} / d

, és követelésünk

\begin{matrix} sin γ = \frac{\sqrt[]{2} c}{d} = \sqrt[]{\frac{2 c^{2}}{a^{2} + b^{2} + c^{2}}} = \sqrt[]{\frac{2}{1 + \frac{a^{2} + b^{2}}{c^{2}}}} < 1, \end{matrix}

ez pedig teljesül, ha

a^{2} + b^{2} > c^{2}

, vagyis ha a vizsgált téglatest leghosszabbik éle kisebb, mint a rá merőleges lap átlója.
Ekkor

\begin{matrix} cos α = \frac{1}{d} \sqrt[]{b^{2} + c^{2} - a^{2}}, cos β = \frac{1}{d} \sqrt[]{c^{2} + a^{2} - b^{2}}, cos γ = \frac{1}{d} \sqrt[]{a^{2} + b^{2} - c^{2}}, \end{matrix}

ezek közül bármelyik kettő meghatározza

e

helyzetét. (Például

D A

és

D B

mint tengely körüli

α

, ill.

β

nyílásszögű kúpfelületeknek negyede esik a

D

-nél levő testszöglet [triéder] belsejébe, ezek egyetlen közös alkotója lesz

e

.)
Nyilvánvalóan megfelel a talált feltételeknek a kocka, és ekkor a testátló egyenese az, amelyre a legnagyobb a távolságösszeg. ‐ De hogy ne mindig csak a legtriviálisabb példákra gondoljunk, vegyük még a csak kevéssel általánosabb

a = b = 5

c = 7

esetet (és állítsuk

c

-t függőlegesnek). Ekkor

α = β

, ezért a maximumot adó egyenes a

D C D^{*} C^{*}

függőleges átlós síkban van, ahol a * (betűvel együtt) az illető csúcs tükörképét jelenti a test centrumára. Továbbá

cos γ = 1 / d

, és a félegyenes egy további,

F

pontját az ábra szerint tűzhetjük ki.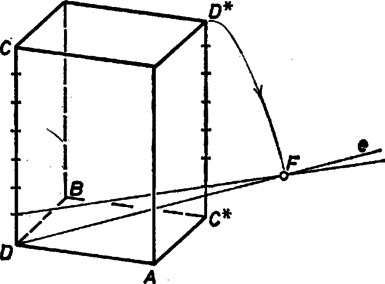

II. megoldás. Jelöljük az

e

egyenesnek az

A D

B D

C D

éllel bezárt szögét rendre

α

-val,

β

-val,

γ

-val. Ekkor az

A

B

, ill.

C

csúcs távolsága az

e

egyenestől rendre

\begin{matrix} a \cdot sin α, b \cdot sin β, c \cdot sin γ . \end{matrix}

Tekintsük a következő két vektort:

\begin{matrix} f = (a, b, c), h = (sin α, sin β, sin γ) . \end{matrix}

Jelöljük az

f

és

h

által bezárt szöget

φ

-vel, így a két vektor skaláris szorzata egyfelől éppen a távolságösszeg, másfelől az ismert képlet alapján:

\begin{matrix} f \cdot h = a sin α + b sin β + c sin γ = | f | \cdot | h | \cdot cos φ = & (*) \\ = \sqrt[]{a^{2} + b^{2} + c^{2}} \cdot \sqrt[]{{sin}^{2} α + {sin}^{2} β + {sin}^{2} γ} \cdot cos φ . \end{matrix}

Mit mondhatunk a

{sin}^{2} α + {sin}^{2} β + {sin}^{2} γ

kifejezésről? Legyen

E

e

egyenes tetszőleges pontja, és vetülete a

D A

D B

D C

élek egyenesére rendre

E_{A}

E_{B}

E_{C}

. Pitagorasz tételét felhasználva

\begin{matrix} {E D}^{2} = {D E}_{A}^{2} + {D E}_{B}^{2} + {D E}_{C}^{2} = {D E}^{2} {cos}^{2} α + {D E}^{2} {cos}^{2} β + {D E}^{2} {cos}^{2} γ \\ 1 = {cos}^{2} α + {cos}^{2} β + {cos}^{2} γ . \end{matrix}

Fölhasználva a

{cos}^{2} x = 1 - {sin}^{2} x

azonosságot, kapjuk

\begin{matrix} 2 = {sin}^{2} α + {sin}^{2} β + {sin}^{2} γ . \end{matrix}

Ezt

(*)

-ba behelyettesítve és fölhasználva, hogy

cos φ ≦ 1

, a bizonyítandó egyenlőtlenséget kapjuk:

\begin{matrix} \sqrt[]{(a^{2} + b^{2} + c^{2}) \cdot 2} \geq a sin α + b sin β + c sin γ . \end{matrix}

Egyenlőség akkor állhat fenn, ha

cos φ = 1

, vagyis az

f

és

h

vektorok egyező irányúak. Mikor lehetséges ez? Ha van olyan

t

pozitív valós szám, amelyre

\begin{matrix} f = h \cdot t \end{matrix}

vagyis

\begin{matrix} \frac{a}{sin α} = \frac{b}{sin β} = \frac{c}{sin γ} = t . \end{matrix}

Ez például teljesül, ha

a = b = c

(vagyis a téglatest kocka) és

sin α = sin β = sin γ

(vagyis

e

éppen a kocka testátlójának egyenese).
Ebből természetesen nem következik, hogy csak ebben az esetben állhat fönn egyenlőség. Csak annyit mutattunk meg, amennyit a feladat kért: lehetséges egyenlőség.