Kezdőlap


Feladat:	F.2211	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Beleznay F. , Bohus G. , Elek G. , Gerencsér Gy. , Gerencsér Gyula , Hegedüs B. T. , Horváth 333 Cs. , Kámán L. , Kántor Zs. , Kiss 352 Gy. , Stark A. , TArdos G. , Tóth V. , Umann G. , Várkonyi B.
Füzet:	1980/január, 6 - 10. oldal		PDF \| MathML
Témakör(ök):	Különleges függvények, Egyenesek egyenlete, Síkbeli ponthalmazok távolsága, Szabályos sokszögek geometriája, Feladat
Hivatkozás(ok):	Feladatok: 1979/szeptember: F.2211

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Válasszuk úgy a koordináta-rendszert, hogy origója a nyolcszög centruma legyen és tengelyei annak átlói legyenek. Jelöljük az $x$ , $y$ tengelyek pozitív felén levő csúcsokat $X$ -szel, $Y$ -nal, az origót $O$ -val, és válasszuk az $O X$ szakasz hosszát egységnek (1. ábra). Írjuk fel először az $X$ -ből az I. negyedbe induló nyolcszögoldal egyenletét.

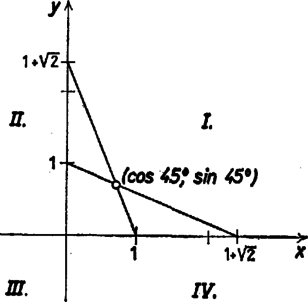1. ábra

X

-szel szomszédos csúcs koordinátái

(cos 45^{\circ}; sin 45^{\circ})

, így az oldal egyenesének az egyenlete

\begin{matrix} y = \frac{\sqrt[]{2}}{\sqrt[]{2} - 2} (x - 1), \end{matrix}

amiből átrendezéssel a

\begin{matrix} \sqrt[]{2} x + (x + y) = \sqrt[]{2} + 1 \end{matrix}

(2)

egyenletet kapjuk. Az ugyancsak az I. negyedben levő, de

Y

-ból induló oldal egyenesének az egyenletét ebből

x

és

y

felcserélésével kapjuk, hiszen ez a két egyenes az

y = x

egyenletű egyenesre nézve szimmetrikusan helyezkedik el. A mondott egyenlet tehát

\begin{matrix} \sqrt[]{2} y + (x + y) = \sqrt[]{2} + 1. \end{matrix}

(3)

Egy egyenletbe foglalhatjuk a két esetet, ha észrevesszük, hogy nekünk akkor van szükségünk (2)-re, amikor

x > y,

és (3)-ra, amikor

y > x

. Így a

\begin{matrix} \sqrt[]{2} {max}_{}^{} (x, y) + (x + y) = \sqrt[]{2} + 1 \end{matrix}

(4)

egyenletet kapjuk, ahol

{max}_{}^{} (x, y)

x

y

számok nagyobbikát jelöli. Ez tehát a

(cos 45^{\circ}, sin 45^{\circ})

pontból induló, az

X

, illetve

Y

ponton átmenő félegyenesek egyesítésének az egyenlete. Nekünk azonban ennek csak az I. negyedbe eső darabja kell, a többi negyedben a megfelelő tengelyekre vonatkozó tükörképekre van szükségünk. Egy csapásra mindkét követelménynek eleget teszünk, ha

x

és

y

helyére azok abszolút értékét írjuk:

\begin{matrix} \sqrt[]{2} {max}_{}^{} (| x |, | y |) + (| x | + | y |) = \sqrt[]{2} + 1. \end{matrix}

(5)

Ez már a nyolcszög egyenlete, de még nem (1) alakú. Vegyük még észre, hogy benne

\begin{matrix} 2 {max}_{}^{} (| x |, | y |) = | x + y | + | x - y |, \end{matrix}

hiszen akármilyen előjelű számokról van is szó, az összegük és különbségük abszolút értéke közül az egyik mindig az abszolút értékek összegével, a másik a nagyobbik és a kisebbik abszolút érték különbségével egyenlő:

\begin{matrix} | x + y | + | x - y | = (| x | + | y |) + {max}_{}^{} (| x |, | y |) - {min}_{}^{} (| x |, | y |) . \end{matrix}

A kapott (5) egyenlet tehát ekvivalens az

\begin{matrix} | x + y | + | x - y | + | \sqrt[]{2} x | + | \sqrt[]{2} y | = 2 + \sqrt[]{2} \end{matrix}

egyenlettel, amiből

10 / (2 + \sqrt[]{2})

-vel való szorzással a keresett (1) alatti alakot kapjuk. Ekkor tehát

n = 4

II. megoldás.

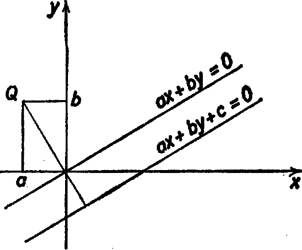2. ábra

Tetszőleges

a

b

c

mellett az

\begin{matrix} F (x, y) = a x + b y + c \end{matrix}

kétváltozós függvény értéke az

\begin{matrix} a x + b y + c = 0 \end{matrix}

egyenletű

e

egyenes pontjaiban

0

-val, az

\begin{matrix} a x + b y + c = d \end{matrix}

egyenletű egyenes pontjaiban

d

-vel egyenlő. Az

F (x, y)

függvény értéke tehát az

e

-vel párhuzamos egyeneseken állandó, vagyis

F (x, y)

értéke egy tetszőleges

P (x; y)

pontban csak attól függ, hogy

P

e

-nek melyik oldalán van, és mennyi

P

és

e

távolsága. Az origón átmenő,

e

-re merőleges egyenes egyenlete

\begin{matrix} b x - a y = 0, \end{matrix}

az ezen levő

Q (a; b)

pontban

F (a, b) = a^{2} + b^{2} + c

, tehát

F (a, b) - F (0, 0) = a^{2} + b^{2}

(2. ábra). Mivel

Q

az origótól

\sqrt[]{a^{2} + b^{2}}

távolságra van, ez azt jelenti, hogy

F

abszolút értéke

P

és

e

távolságának

\sqrt[]{a^{2} + b^{2}}

-szerese. Ezzel beláttuk, hogy a

P (x, y)

távolsága az

a_{i} x + b_{i} y + c_{i} = 0

egyenletű

e_{i}

egyenestől, amit

d_{i} (P)

-vel jelölünk

\begin{matrix} d_{i} (P) = \frac{| a_{i} x + b_{i} y + c_{i} |}{\sqrt[]{a_{i}^{2} + b_{i}^{2}}} . \end{matrix}

A továbbiakban feltesszük, hogy

\sqrt[]{a_{i}^{2} + b_{i}^{2}}

értéke

i

-től függetlenül állandó, és jelöljük

10 / d

-vel. Ezzel a megszorítással a feladatot a következő alakba írhatjuk át:
Keressünk a síkon

n

egyenest és egy

d

távolságot úgy, hogy azon

P

pontok mértani helye a síkban, melyekre az egyenesektől mért távolságösszeg éppen

d

, azaz melyekre

\begin{matrix} \sum_{i = 1}^{n} d_{i} (P) = d, \end{matrix}

egy szabályos nyolcszög pontjai.
a) Ha az

e_{1}

és

e_{2}

párhuzamos egyenesek távolsága

t_{12}

, akkor a sík tetszőleges

P

pontjára

\begin{matrix} d_{1} (P) + d_{2} (P) \geq t_{12}, \end{matrix}

és egyenlőség akkor és csak akkor áll, ha a

P

pont a két egyenes valamelyikén, vagy a két egyenes között helyezkedik el. Így ha

e_{1}

és

e_{2}

;

e_{3}

és

e_{4}

;

e_{5}

és

e_{6}

, valamint

e_{7}

és

e_{8}

egyenesek (páronként) párhuzamosak, távolságuk pedig rendre

t_{12}

t_{34}

t_{56}

és

t_{78}

, akkor

\begin{matrix} \sum_{i = 1}^{8} d_{i} (P) \geq t_{12} + t_{34} + t_{56} + t_{78}, \end{matrix}

és egyenlőség csak akkor áll, ha a

P

pont mind a négy párhuzamos egyenespár között (a határokat is beleértve) helyezkedik el. Ez azt jelenti, hogy ha

e_{1}

és

e_{2}

;

e_{3}

és

e_{4}

stb. egy szabályos nyolcszög szemben levő oldalegyenesei, akkor

t_{12} = t_{34} = t_{56} = t_{78}

, és a

\begin{matrix} \sum_{i = 1}^{8} d_{i} (P) = 4 t_{12} = d \end{matrix}

összefüggés csak a nyolcszög belső- és határpontjaira teljesül. Például ha a nyolcszög oldalegyenesei a 3. ábrán látható egyenesek, akkor

\begin{matrix} | x + \frac{5}{4} | + | x - \frac{5}{4} | + | y + \frac{5}{4} | + | y - \frac{5}{4} | + | \frac{x}{\sqrt[]{2}} + \frac{y}{\sqrt[]{2}} + \frac{5}{4} | + | \frac{x}{\sqrt[]{2}} + \frac{y}{\sqrt[]{2}} - \frac{5}{4} | + \\ + | \frac{x}{\sqrt[]{2}} - \frac{y}{\sqrt[]{2}} + \frac{5}{4} | + | \frac{x}{\sqrt[]{2}} - \frac{y}{\sqrt[]{2}} - \frac{5}{4} | = 10 \end{matrix}

feltételeknek eleget tevő

(x, y)

számpárok a nyolcszög belső és határpontjait adják.

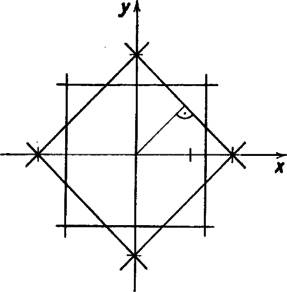3. ábra

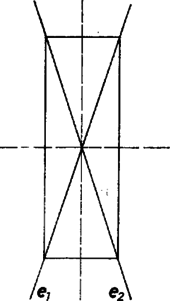4. ábra

b) Ha az

e_{1}

és

e_{2}

egyenesek az

O

pontban metszik egymást, akkor azon

P

pontok mértani helye, melyekre

d_{1} (P) + d_{2} (P) = t

(adott szakasz), egy téglalap (4. ábra), melynek oldalai párhuzamosak a két egyenes szögfelezőivel. Ez az állítás azonnal következik abból az ismert tételből, hogy egyenlő szárú háromszög alapján levő tetszőleges pontnak a száraktól mért távolságainak összege állandó (5. ábra).

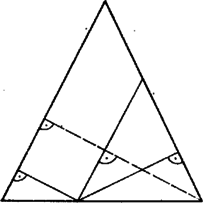\begin{matrix} \sum_{i = 1}^{8} d_{i} (P) \geq t_{12} + t_{34} + t_{56} + t_{78}, \end{matrix}

5. ábra

Ennek alapján ha

e_{1}

e_{2}

e_{3}

és

e_{4}

egymásból pozitív irányú

45^{\circ}

-os elforgatással kapható, akkor azon

P

pontok, amelyekre

\begin{matrix} \sum_{i = 1}^{4} d_{i} (P) = d \end{matrix}

(6)

teljesül, és az

e_{2}

és

e_{3}

egyenesek közti kisebbik szögtartományban vannak (6. ábra), két, egymással szimmetrikus helyzetű, az

f

szögfelezőre merőleges szakaszon helyezkednek el, hiszen

f

e_{1}

és

e_{4}

szögfelezője is. Így a (6) feltételt kielégítő pontok szabályos nyolcszög határpontjait alkotják. A mondottak alapján a

\begin{matrix} | \sqrt[]{2} x | + | \sqrt[]{2} y | + | x + y | + | x - y | = 10 \end{matrix}

feltételt egy szabályos nyolcszög határpontjai elégítik ki.

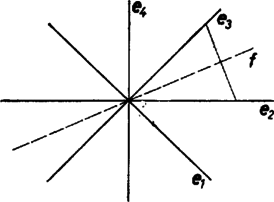6. ábra

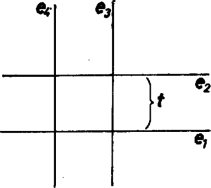7. ábra

Hasonló meggondolás mutatja, hogy például egy

t

oldalú négyzet oldalegyeneseitől mért

d = (2 + \sqrt[]{2}) t

távolságösszegű pontok is szabályos nyolcszög határpontjait határozzák meg (7. ábra), ami az

α = \frac{5}{2} (2 - \sqrt[]{2})

jelöléssel az

\begin{matrix} | x + α | + | x - α | + | y + α | + | x - α | = 10 \end{matrix}

feltételt adja. Ezeken kívül a feladatnak sok más megoldása lehetséges.

Gerencsér Gyula (Zalaegerszeg, Ságvári E. Gimn., III. o. t.)
dolgozata alapján