Kezdőlap


Feladat:	F.2208	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	1979/november, 140 - 142. oldal		PDF \| MathML
Témakör(ök):	Alakzatba írt kör, Beírt gömb, Szélsőérték differenciálszámítással, Szabályos sokszög alapú gúlák, Egyenlő szárú háromszögek geometriája, Feladat
Hivatkozás(ok):	Feladatok: 1979/május: F.2208

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a kérdéses alapot $2 x$ -szel, így a beírt kör $ϱ$ sugarának ismert $t / s$ kifejezése céljára a háromszög területe $t = x \sqrt[]{1 - x^{2}}$ , kerülete $2 x + 2$ , tehát a vizsgálandó függvény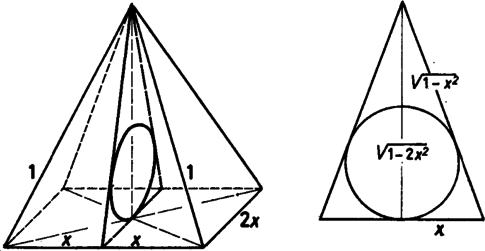

\begin{matrix} ϱ = \frac{t}{s} = \frac{x \sqrt[]{1 - x^{2}}}{1 + x} = \sqrt[]{\frac{x^{2} - x^{3}}{1 + x}}, \end{matrix}

és a háromszög-egyenlőtlenség alapján

0 < x < 1

Mivel

ϱ > 0

, és pozitív szám négyzete monoton nő, azért

ϱ

-nak ugyanott van maximuma, ahol

ϱ^{2}

-nek, ezért elég vizsgálnunk a következő függvényt:

\begin{matrix} ϱ^{2} = f (x) = \frac{x^{2} - x^{3}}{1 + x} . \end{matrix}

Deriváltja, mindjárt átalakításokkal:

\begin{matrix} f' (x) = \frac{(2 x - 3 x^{2}) (1 + x) - (x^{2} - x^{3})}{{(1 + x)}^{2}} = \frac{2 x (1 - x - x^{2})}{{(1 + x)}^{2}} = \\ = \frac{x (\frac{\sqrt[]{5} - 1}{2} - x) (\sqrt[]{5} + 1 + 2 x)}{{(1 + x)}^{2}}, \end{matrix}

az értelmezési tartomány minden helyén létezik.

f (x)

csakis az

\begin{matrix} x_{0} = \frac{\sqrt[]{5} - 1}{2} (= 0, 618 ...) \end{matrix}

helyen tűnik el, és itt áthaladva, az utolsó alakban a számláló első zárójele vált előjelet, pozitívból negatívvá válik, a többi tényező pozitív.
Eszerint

ϱ^{2}

és

ϱ

értéke az

x_{0}

-on áthaladva növekedésből csökkenésbe megy át, ott maximum van. És mivel ekkor az alapél

2 x_{0} \neq 1

, az állítás első részét bebizonyítottuk. (Valóban,

x_{0}

mellett

ϱ = 0, 3003

2 x = 1

mellett viszont csak

ϱ = \sqrt[]{3} / 6 = 0, 2887

.)
2. Messük a gúlát a tengelyen átmenő és valamelyik alapélére merőleges

S

síkkal. Ez nyilvánvalóan szimmetriasíkja a gúlának, ennélfogva a beírt gömbnek az átmetszett oldallapokkal való érintkezési pontjai benne vannak

S

-ben.

S

a gúlából egyenlő szárú háromszöget metsz ki, melynek szárai az oldallapok

o_{m}

magasságai, a beírt gömbből pedig egy főkört, és ez a főkör éppen a kimetszett háromszög beírt köre.
A gúla alapélét ismét

2 x

-szel jelölve a föntebbi számítás az alábbiak szerint módosul. A metszetháromszög szárainak hossza (a fönti

1

helyén)

\sqrt[]{1 - x^{2}}

, így a háromszög magassága

\sqrt[]{1 - 2 x^{2}}

, kerülete

2 x + 2 \sqrt[]{1 - x^{2}}

. Ezekből

\begin{matrix} ϱ = \frac{x \sqrt[]{1 - 2 x^{2}}}{\sqrt[]{1 - x^{2}} + x}, ahol 0 < x < \frac{1}{\sqrt[]{2}} (= 0, 707) . \end{matrix}

Belátjuk, hogy

ϱ = f (x)

az értelmezési tartományában folytonos függvénye az

x

-nek. Valóban, ez áll a kifejezés

x

\sqrt[]{1 - x^{2}}

\sqrt[]{1 - 2 x^{2}}

elemeire, így a számlálóra és a nevezőre is, és mivel a nevező sehol sem

0

az intervallumban, azért a hányadosra is.
Így elég mutatni egy olyan

x_{1}

értéket, amely mellett

ϱ

-ra nagyobb értéket kapunk, mint

x = 0, 5

mellett, és egy olyan

x_{2}

értéket, ahol

ϱ

kisebbnek adódik, mint

x = 0, 5

mellett, hacsak az (

x_{1}

x_{2}

) intervallum tartalmazza az

x = 0, 5

helyet. Megfelel erre

\begin{matrix} x_{1} = 0, 48 és x_{2} = 0, 52, \end{matrix}

ugyanis az elsőt lekerekítve, a másodikat fölkerekítve

\begin{matrix} f (x_{1}) = 0, 2597, f (0, 5) = 0, 2588, f (x_{2}) = 0, 2564, \end{matrix}

ezzel megmutattuk, hogy a feladat 2. állítása is helyes.
Bonyolultabb számítással meg lehet mutatni, hogy

ϱ

x = 0, 4776

és

x = 0, 4777

helyek közt veszi fel legnagyobb értékét, és az

0, 2597

Megjegyzés. Ismét

ϱ^{2}

maximumhelyét keressük, kifejezését így alakítjuk:

\begin{matrix} ϱ^{2} = g (x) = \frac{x^{2} (1 - 2 x^{2})}{1 + 2 x \sqrt[]{1 - x^{2}}} = \frac{x^{2} (1 - 2 x^{2}) (1 - 2 x \sqrt[]{1 - x^{2}})}{1 - 4 x^{2} (1 - x^{2})} . \end{matrix}

A nevező

{(1 - 2 x^{2})}^{2}

, és mivel

ϱ

kifejezésében kikötöttük, hogy

1 - 2 x^{2} > 0

, azért egyszerűsíthetünk:

\begin{matrix} g (x) = \frac{x^{2} (1 - 2 x \sqrt[]{1 - x^{2}})}{1 - 2 x^{2}} . \end{matrix}

[A számláló is pozitív, mert

x = sin z

(ahol

0^{\circ} < z < 45^{\circ}

) helyettesítéssel

(1 - sin 2 z)

alakba írható.]
Felírjuk

g' (x)

-et és megmutatjuk, hogy

g' (0, 5) < 0

, ebből már következik a feladat állítása. A 2192. feladatban látott

(u v)' = u' v + u v'

deriválási szabályhoz hasonlóan lehet belátni, hogy ha

u

és

v

deriválhatók egy intervallumban és ugyanott

v \neq 0

, akkor

\begin{matrix} (\frac{u}{v})' = \frac{u' v - u v'}{v^{2}} . \end{matrix}

Esetünkben

v = 1 - 2 x^{2} > 0

, továbbá a számlálóban

\begin{matrix} (1 - 2 x \sqrt[]{1 - x^{2}})' = - 2 \sqrt[]{1 - x^{2}} + \frac{2 x^{2}}{\sqrt[]{1 - x^{2}}} = \frac{- 2 + 4 x^{2}}{\sqrt[]{1 - x^{2}}} = - \frac{2 (1 - 2 x^{2})}{\sqrt[]{1 - x^{2}}} . \end{matrix}

(tovább is alkalmazzuk a látott közös nevezőre hozást), így a számláló deriváltja, majd a nevezőé:

\begin{matrix} u' = 2 x (1 - 2 x \sqrt[]{1 - x^{2}}) - \frac{2 x^{2} (1 - 2 x^{2})}{\sqrt[]{1 - x^{2}}} = 2 x + \frac{8 x^{4} - 6 x^{2}}{\sqrt[]{1 - x^{2}}}, ill. v' = - 4 x . \end{matrix}

Ezeket beírva,

g' (x)

számlálója,

\begin{matrix} u' v - u v' = 2 x - 4 x^{3} + \frac{- 16 x^{6} + 20 x^{4} - 6 x^{2}}{\sqrt[]{1 - x^{2}}} + 4 x^{3} + \frac{8 x^{6} - 8 x^{4}}{\sqrt[]{1 - x^{2}}} = \\ = 2 x - \frac{8 x^{6} - 12 x^{4} + 6 x^{2}}{\sqrt[]{1 - x^{2}}} . \end{matrix}

[Nincs szükség

g' (0, 5)

előjelének megállapításához a nevezőre, mert az pozitív.] A kapott kifejezés értéke pedig

2 x = 1

helyettesítéssel:

\begin{matrix} 1 - \frac{7}{4 \sqrt[]{3}} = 1 - \sqrt[]{\frac{49}{48}} < 0, \end{matrix}

ezt akartuk belátni.