Kezdőlap


Feladat:	F.2203	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Benedek Ágnes , Bukta Gy. , Csordás A. , Feledi Gy. , Hajnal P. , Hochenburger R. , Horváth Cs. , Kántor Zs. , Kassai J. , Király E. , Kovács 134 I. , Mala J. , Márkus L. , Németh Ágnes , Pintér F. , Porcsalmi L. , Ruisz T. , Soós Marianna , Sz. Nagy Cs. , Szegedy P. , Szeles J. , Tálas Cs. , Varga J. , Varga Lívia , Varga T. , Veres Pál
Füzet:	1979/november, 133 - 135. oldal		PDF \| MathML
Témakör(ök):	Trigonometriai azonosságok, Hiperbola egyenlete, Paralelogrammák, Koszinusztétel alkalmazása, Feladat
Hivatkozás(ok):	Feladatok: 1979/április: F.2203

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen az $A B C D$ paralelogrammában $A C = e$ , $B A - B C = d$ , az így fölvett $B A > B C$ nagyságviszony folytán és $φ < 90^{\circ}$ föltételezésével ( $φ$ a $B O C$ szöget jelenti, ahol $O$ az idom középpontja). Legyen továbbá $B C = a$ , $B D = f$ .

A cosinustétel alkalmazásával az

A O B

háromszögből

\begin{matrix} {(a + d)}^{2} = \frac{e^{2} + f^{2}}{4} + \frac{e f}{2} cos φ, \end{matrix}

B O C

háromszögből

\begin{matrix} a^{2} = \frac{e^{2} + f^{2}}{4} - \frac{e f}{2} cos φ, \end{matrix}

ezekből összeadással és kivonással

\begin{matrix} 2 a^{2} + 2 a d + d^{2} = \frac{e^{2} + f^{2}}{2}, \\ 2 a d + d^{2} = e f cos φ = g f, \end{matrix}

ahol rövidítésül

g = e cos φ

. Az utóbbiakból

f

kiküszöbölésével, majd rendezéssel

\begin{matrix} f^{2} = 4 a^{2} + 4 a d + 2 d^{2} - e^{2} = \frac{1}{g^{2}} {(2 a d + d^{2})}^{2} \\ a^{2} + d a - \frac{g^{2} (e^{2} - 2 d^{2}) + d^{4}}{4 (g^{2} - d^{2})} = 0. & (1) \end{matrix}

A gyökök valósak, ha a diszkrimináns

\begin{matrix} d^{2} + \frac{g^{2} (e^{2} - 2 d^{2}) + d^{4}}{g^{2} - d^{2}} = \frac{g^{2} (e^{2} - d^{2})}{g^{2} - d^{2}} \end{matrix}

pozitív. Ehhez ‐ mivel

g < e

‐, elegendő, hogy a nevezőben

d < g = e cos φ

, azaz

cos φ > d / e

legyen. (Különben a

φ

-től függetlenül is, az

A B C

részháromszög létrejövéséhez szükséges, hogy

d < e

legyen.) Ha ez teljesül, akkor (1)-nek csak a nagyobbik gyöke pozitív, hiszen a két gyök összege:

- d < 0

, a megoldás egyértelmű.
Áttérve az

A B C ∢ = β

kiszámításának kérdésére, érdekes észrevételt tehetünk. A cosinustételt az

A B C

háromszögre alkalmazva

\begin{matrix} cos β = \frac{a^{2} + {(a + d)}^{2} - e^{2}}{2 a (a + d)} = 1 - \frac{e^{2} - d^{2}}{2 (a^{2} + a d)}, \end{matrix}

és itt a zárójelben (1) bal oldalának első két tagja áll, tehát helyettesíthető az

a

-t nem tartalmazó tag

(- 1)

-szeresével. Ennek alapján

β

kiszámításával meg is előzhetjük az oldalakét:

\begin{matrix} cos β = 1 - \frac{2 (e^{2} - d^{2}) (g^{2} - d^{2})}{g^{2} (e^{2} - 2 d^{2}) + d^{4}} . \end{matrix}

Számadatainkkal (1) pozitív gyöke

a = 23, 95

, a hosszabb oldal

33, 95

egység, végül

β = 49^{\circ} 46'

Megjegyzés. Ugyanezen adatokból szerkesztéssel állítottuk elő a paralelogrammát az 1773. sz. gyakorlatban ‐ K. M. L. 57 (1978) 213. oldal. Az itt többször használt

g

szakasz az ottani

O C'

-nek a 2-szerese. Gondoljanak utána az érdeklődők: hogyan lehetne számítással követni a szerkesztés lépéseit.

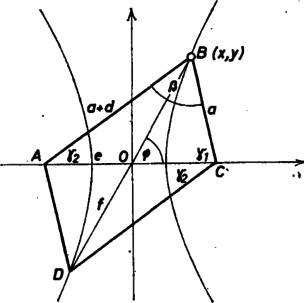
II. megoldás. Válasszuk derékszögű koordináta-rendszerünk

x

-tengelyéül az

A B C D

paralelogramma adott hosszúságú

A C = e

átlójának egyenesét és origónak az idom középpontját; így

A

(

- e / 2

0

) és

C

(

e / 2

0

). Teljesüljön továbbá az idom

B

(

x

y

) csúcsára

x > 0

és

y > 0

. Eszerint

B A > B C

, és így

B A - B C = d

, koordinátákkal kifejezve, majd négyzetre emelés és rendezés után:

\begin{matrix} \sqrt[]{{(x + \frac{e}{2})}^{2} + y^{2}} = d + \sqrt[]{{(x - \frac{e}{2})}^{2} + y^{2}}, \\ 2 e x - d^{2} = 2 d \sqrt[]{{(x - \frac{e}{2})}^{2} + y^{2}}, \end{matrix}

újabb négyzetre emelés és átrendezés után

\begin{matrix} \frac{4 x^{2}}{d^{2}} - \frac{4 y^{2}}{e^{2} - d^{2}} = 1. \end{matrix}

(2)

A négyzetre emelések nyomán itt

x

és

y

, másrészt

d

és

e

is páros kitevővel szerepel, emiatt ha

B

(

x

y

) kielégíti ezt, akkor

D

(

- x

- y

) is, továbbá a tengelyekre való tükörképeik is, amelyekre

B' A - B' C = - d

. (

e

előjelváltása ugyanezt adja

A

és

C

fölcserélésével.) Ez tulajdonképpen az

A

C

fókuszpárral és a

d

valós tengelyhosszal meghatározott hiperbola egyenlete.
A

B D

átlóegyenes egyenlete

y = x \cdot tg φ

, ennek alapján (1)-ből

B

koordinátái goniometrikus átalakításokkal és az

f

rövidítést bevezetve

\begin{matrix} x = \frac{d \sqrt[]{e^{2} - d^{2}} cos φ}{2 \sqrt[]{e^{2} cos^{2} φ - d^{2}}} = \frac{f}{2} cos φ (> 0), y = \frac{f}{2} sin φ (> 0) . \end{matrix}

Könnyű észrevenni, hogy itt

\begin{matrix} f = \frac{d \sqrt[]{e^{2} - d^{2}}}{\sqrt[]{e^{2} cos^{2} φ - d^{2}}} \end{matrix}

éppen a

B D

átló hosszát jelenti. Megoldás van, ha

d < e cos φ (< e)

.
Tovább menve, a már fölírt kifejezésből

\begin{matrix} B C = \sqrt[]{{(x - \frac{e}{2})}^{2} + y^{2}} = \frac{1}{2} \sqrt[]{{(f cos φ - e)}^{2} + {(f sin φ)}^{2}} = \frac{1}{2} \sqrt[]{f^{2} + e^{2} - 2 e f cos φ}, \end{matrix}

azonos a

C O B

háromszögből a cosinustétel révén adódó kifejezéssel. A másik oldal ismét

B A = d + B C

.
Végül a paralelogramma szögét a

C B

és

A B

félegyenesek iránytangenseiből kapjuk:

\begin{matrix} tg (180^{\circ} - γ_{1}) = \frac{y}{x - \frac{e}{2}}, tg γ_{2} = \frac{y}{x + \frac{e}{2}}, \end{matrix}

és ezekből

B C D ∢ = γ_{1} + γ_{2}

.
A feladat számadataival

f = 52, 70

x = 11, 14

y = 23, 88

B C = 23, 95

B A = 33, 95

B C D ∢ = 85, 55^{\circ} + 44, 69^{\circ} = 130, 24^{\circ}

, a hegyesszög pedig

49,76^{\circ} = 49^{\circ} 46^{,}