Kezdőlap


Feladat:	F.2202	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Balogh S. , Barla F. , Beleznay F. , Bereznai M. , Bozsó P. , Bukta Gy. , Cseri I. , Elter J. , Erdélyi T. , Gajdos S. , Golarits I. , Gombás L. , Horányi T. , Kántor Zs. , Karakas J. , Károlyi Gy. , Király Z. , Komlósi Erzsébet , Kőrössy Katalin , Kovács 134 I. , Kozák Ágnes , Krausz F. , Liszkai S. , Mala J. , Márkus L. , Matlák T. , Misota G. , Pátkai Andrea , Ruisz T. , Seres I. , Szabó Elemér , Szabó Endre , Szegedy P. , Takáts L. , Tóth 397 J. , Trauttwein A. , Umann G. , Varga Ildikó , Varga Lívia , Vida J. , Winkler R. , Zakar L. , Zsilinszky L.
Füzet:	1979/november, 131 - 132. oldal		PDF \| MathML
Témakör(ök):	Trigonometriai azonosságok, Derékszögű háromszögek geometriája, Szélsőérték-feladatok differenciálszámítás nélkül, Háromszögek szerkesztése, Feladat
Hivatkozás(ok):	Feladatok: 1979/április: F.2202

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Tegyük fel a kérdést ebben a fordított megfogalmazásban: eljuthat-e a $P$ pont az $A C$ szakasz tetszőleges $P^{*}$ pontjába? A választ a $P$ -t előállító eljárás megfordításával készítjük elő. Messe $A B$ -t a $P^{*}$ -ban $A C$ -re állított merőleges $N^{*}$ -ban. $P^{*}$ -ot akkor és csak akkor éri el $P$ , ha van $A$ C-n olyan $M^{*}$ pont, amelyből az $N^{*} B$ szakasz derékszögben látható; más szóval: ha az $N^{*} B$ átmérőjű $k^{*}$ Thalész-körnek van közös pontja $A C$ -vel. Tovább csak ilyen $P^{*}$ -okkal foglalkozunk.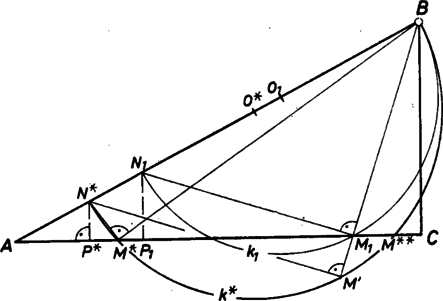

1. ábra

Megmutatjuk, hogy ha két közös pontja van

k^{*}

-nak és

A C

-nek:

M^{*}

és

M^{* *}

úgy, hogy

A M^{*} < A M^{* *}

, akkor

C

-nek a

P^{*}

által elért megközelítése javítható,

A C

-nek bármely, az

M^{*}

és

M^{* *}

közti

M_{1}

pontjához olyan

P_{1}

tartozik, amelyre

C P_{1} < C P^{*}

. ‐ Könnyű belátni, hogy mindkét közös pont

A

és

C

között van, tehát

M_{1}

is. Tekintsük azt a

k_{1}

kört, amelynek

O_{1}

középpontja az

A B

egyenesen van és amely átmegy

M_{1}

-en és

B

-n; legyen az

M_{1}

-ből képezett pont

N_{1}

, továbbá messe a

B M_{1}

egyenes

k^{*}

-ot

M'

-ben. Így a hasonló

B N_{1} M_{1}

és

B N^{*} M'

derékszögű háromszögekből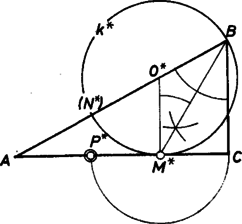

\begin{matrix} B N_{1} = \frac{B M_{1}}{B M'} \cdot B N^{*} < B M^{*}, \end{matrix}

hiszen

M_{1}

k^{*}

belsejében van, tehát

B M' > B M_{1}

. Ekkor pedig a két átmérő

A C

-n levő vetületeire

C P_{1} < C P^{*}

, amint állítottuk.

2. ábra

Ezek szerint csak akkor nem javítható

C

-nek

P^{*}

által elért megközelítése ‐ vagyis akkor a legjobb ‐, ha

k^{*}

-nak pontosan egy közös pontja van

A C

-vel, ha

M^{*}

-ban érintkeznek. Ekkor az

M^{*} O^{*}

sugár merőleges

A C

-re és párhuzamos

B C

-vel, az

M^{*} B O^{*}

háromszög egyenlő szárú (2. ábra):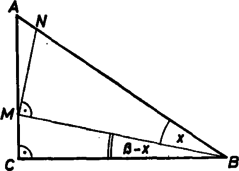

\begin{matrix} A B M^{*} C ∢ = B M^{*} O^{*} ∢ = M^{*} B C ∢, \end{matrix}

a kérdéses

P^{*}

pontot előállító

M^{*}

pontra

M^{*} B

felezi az

A B C

szöget. Ekkor

P^{*}

megszerkesztésében

N^{*}

mellőzhető,

M^{*} O^{*} | | C B

és

B N^{*} = 2 \cdot B O^{*}

alapján

P^{*}

C

-nek

M^{*}

-ra való tükörképe.

A szögfelező osztásarány-tétele alapján az

A B C

háromszög oldalait szokásosan jelölve

\begin{matrix} C P^{*} = 2 C M^{*} = \frac{2 a b}{a + c}, \end{matrix}

ekkora a

C P

távolság minimuma.

II. megoldás.

P

definíciójából következik, hogy keresett helyzetében

N

is legközelebb esik

B

-hez, elég meghatároznunk a minimális

B N

-re vezető

M

pontot. Jellemezzük ennek helyzetét az

A B M ∢ = x

szöggel. Ekkor

M B C ∢ = β - x

, és ismert azonosság alkalmazásával (3. ábra):

\begin{matrix} B N = \frac{B M}{cos x} = \frac{B C}{cos (β - x) cos x} = \frac{2 a}{cos β + cos (β - 2 x)} \geq \frac{2 a}{cos β + 1} . \end{matrix}

3. ábra

Egyenlőség létre is jöhet, éspedig akkor, ha

cos (β - 2 x) = 1

, vagyis

x = β / 2

.
Tovább az I. megoldás szerint haladhatunk.