Kezdőlap


Feladat:	F.2185	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bedő Katalin , Benkő B. , Braun E. , Bölcsföldi L. , Csordás A. , Dénes L. , Guba L. , Hajnal P. , Horváth T. , Kántor Zs. , Kiss Gy. , Kurusa Á. , Nagy 647 Gábor , Pátkai Andrea , Sz. Nagy Cs. , Szegedy P. , Tóth J. , Varga Lívia , Varga T.
Füzet:	1979/május, 205 - 208. oldal		PDF \| MathML
Témakör(ök):	Háromszögek nevezetes tételei, Terület, felszín, Deltoidok, Négyszögek geometriája, Vektorok lineáris kombinációi, Feladat
Hivatkozás(ok):	Feladatok: 1979/január: F.2185

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük a $B C$ , $D A$ egyenesek metszéspontját $E$ -vel, $A B$ , $C D$ metszéspontját $F$ -fel, és tegyük fel, hogy $E$ az $A B$ , $F$ az $A D$ egyenes $C$ -vel ellentétes oldalán jön létre. Ez utóbbi feltevésnek nincs jelentősége, hiszen a feladat állításában a négyszög csúcsai egyenrangú szerepet játszanak.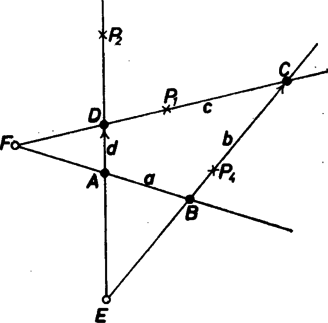

Legyen továbbá

\begin{matrix} a = \frac{A B}{F B}, b = \frac{B C}{E C}, c = \frac{C D}{C F}, d = \frac{D A}{D E} . \end{matrix}

Ha a

C D E

háromszög területét

T

-vel jelöljük, akkor

\begin{matrix} 2 t = [1 - (1 - b) (1 - d)] T, \end{matrix}

és az

A D P_{4}

háromszög területe

\begin{matrix} t = [1 - (1 - d)] λ_{4} T, \end{matrix}

ahol

λ_{4} = \frac{E P_{4}}{E C}

. E két összefüggés alapján

λ_{4}

értéke

\begin{matrix} λ_{4} = \frac{b + d - b d}{2 d} . \end{matrix}

Hasonlóan kapjuk a

λ_{2} = \frac{E P_{2}}{E D}

λ_{1} = \frac{F P_{1}}{F C}

hányadosok értékét:

\begin{matrix} λ_{2} = \frac{b + d - b d}{2 b}, λ_{1} = \frac{a + c - a c}{2 a} . \end{matrix}

Azt fogjuk megmutatni, hogy

P_{1}

rajta van a

P_{2} P_{4}

egyenesen; azt, hogy

P_{3}

is rajta van ezen, hasonlóan láthatnánk be. Mivel

P_{1}

C D

szakaszt

(1 - λ_{1}) : (λ_{1} + c - 1)

arányban osztja,

\begin{matrix} {\vec{E P}}_{1} = \frac{1 - λ_{1}}{c} \vec{E D} + \frac{λ_{1} + c - 1}{c} \vec{E C} = \frac{1 - λ_{1}}{c λ_{2}} {\vec{E P}}_{2} + \frac{λ_{1} + c - 1}{c λ_{4}} {\vec{E P}}_{4} . \end{matrix}

Ismeretes, hogy

P_{1}

akkor és csakis akkor van rajta a

P_{2} P_{4}

egyenesen, ha itt az együtthatók összege 1. Eszerint azt kell megmutatnunk, hogy

\begin{matrix} (1 - λ_{1}) (λ_{4} - λ_{2}) + c λ_{2} (1 - λ_{4}) = 0. \end{matrix}

Behelyettesítve a

λ_{i}

arányok értékét, a lehetséges egyszerűsítések után ebből az

\begin{matrix} (\frac{1}{a} - \frac{1}{c}) (\frac{1}{d} - \frac{1}{b}) = 1 \end{matrix}

összefüggést kapjuk.
Jelöljük az

E F C

háromszög területét

τ

-val. Akkor

F B C

területe

b τ

F A C

területe pedig

(1 - a) b τ

. Mivel

F A C

és

E F C

egy oldala közös, és a megfelelő magasságok aránya

d : 1

, ebből kapjuk, hogy

\begin{matrix} b = \frac{d}{1 - a} . \end{matrix}

Hasonlóan kapjuk, hogy

\begin{matrix} c = \frac{a}{1 - d}, \end{matrix}

és ezeket a bizonyítandó összefüggésbe helyettesítve valóban azonosságot kapunk.

II. megoldás. Próbát téve a nem kizárt négyszögek legszabályosabbikával, a deltoiddal, az állítás szerinti egyenesként az idom tengelye adódik, két-két

P

pont egybeesik a tengely végpontjaival. Ezt találjuk a ferdén szimmetrikus négyszögnél is, ti. amelyben az egyik átló felezi a másikat. Azt sejtjük további vázlatokból is, hogy a kérdéses egyenes felezi az átlókat (és még a szemben fekvő oldalegyenes-párok metszéspontjai közti szakaszt is). Megfordítva azt fogjuk bizonyítani, hogy a

P_{i}

pontokat

(i = 1,2,3,4)

az átlók felezőpontjaival meghatározott egyenes metszi ki az oldalegyenesekből. Ez az egyenes egyértelműen meg van határozva, hiszen a kiindulás kizárta a vizsgálatból a paralelogrammákat. Még trapézokra sem vonatkozik az állítás, így mindegyik

P

egyértelmű létezése is biztos, hiszen ha pl. az

A B

és

C D

egyenesek metszéspontja

M

, és egy

P

pont az

M C

félegyenesen fut, eközben az

A B P

háromszög területe minden pozitív értéket fölvesz.
A bizonyítást lényegében csak

P_{1}

-re végezzük el, és a szemléletesség érdekében ehhez igazítjuk a csúcsok betűzését. Legyen az átlók metszéspontja

O

, ez egyik átlót se felezze (hiszen már láttuk azt az esetet, ha az egyiket felezi), az átlók nagyobbik darabjának végpontja

A

, ill.

D

, így a sejtésünk szerinti egyenes

A B

-n és

D C

-n át lép ki a négyszögből, az utóbbiról mutatjuk meg, hogy ez a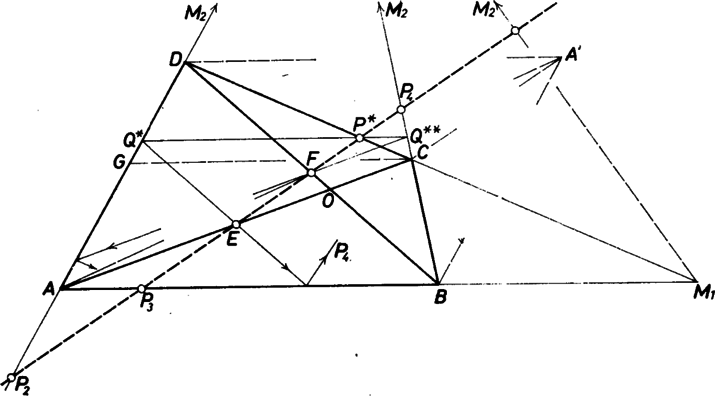

P_{1}

A sejtésünktől függetlenül abból az észrevételből kaphatjuk meg

P_{1}

-et, hogy a

B E D

töröttvonal két egyenlő területű részre vágja a négyszöget: meghúzzuk

E

-n át a párhuzamost

B D

-vel

A D

-nek

Q

pontjáig (

A

és

D

között), innen pedig

A B

-vel haladunk párhuzamosan a

C D

-vel való metszéspontig. Ekkor ugyanis a területekre

\begin{matrix} A B P_{1} = & A B Q = B D A - B D Q = B D A - B D E = A B E D = A E B + A E D = & (1) \\ = \frac{A C B}{2} + \frac{A C D}{2} = \frac{1}{2} A B C D = t . \end{matrix}

Ennek megfordítását járjuk végig a bizonyításban:

E F

és

C D

közös

P^{*}

pontjából visszafelé szerkesztjük

Q^{*}

-ot:

Q^{*} P^{*} ∥ A B

, és belátjuk, hogy

Q^{*} E ∥ B D

. Ennek során

P^{*}

és

Q^{*}

helyzetét előbb szakaszok arányával jellemezzük, majd ezekből áttérünk alkalmas háromszögek területeinek arányára. Legyen még

A

-nak

F

-re való tükörképe

A'

, továbbá messe a

C

-n átmenő,

A B

-vel párhuzamos egyenes

A D

-t

G

-ben. Így

A B A' D

paralelogramma és

C A' = 2 \cdot E F

, párhuzamosak is; e két szakasszal szorozzuk alább a nevezőt, ill. a számlálót. Szerkesztéseink szerint egyrészt

\begin{matrix} \frac{Q^{*} D}{G D} = \frac{P^{*} D}{C D} = \frac{2 \cdot P^{*} D \cdot E F}{C D \cdot C A'} = \frac{2 \cdot D F E}{D A' C} = \frac{D B E}{D A' G} . \end{matrix}

(

P^{*} D

és

C D

nem magasságok e háromszögekben az

E F

, ill.

C A'

alaphoz képest, de arányosak a megfelelő magasságokkal, mert egyenlő szöggel hajlanak azokhoz. Ezzel használtuk ki, hogy

P^{*}

E F

egyenesen van.) Másrészt hasonlóan

\begin{matrix} \frac{D G}{D A} = \frac{D A' G}{D A' A} = \frac{D A' G}{D B A}, \end{matrix}

végül e kettőt összeszorozva

G D

kiesik:

\begin{matrix} \frac{D Q^{*}}{D A} = \frac{D B Q^{*}}{D B A} = \frac{D B E}{D B A} . \end{matrix}

Ez pedig azt jelenti, hogy

Q^{*}

és

E

valóban egyenlő távolságra vannak

D B

-től.
Megkaphattuk volna

P_{1}

-et

F

-ből kiindulva is,

F

-ből

A C

-vel párhuzamosan haladunk

B C

-nek

Q^{* *}

pontjáig és onnan ismét

A B

-vel párhuzamosan. Ábránkon

Q^{* *}

B C

oldal meghosszabbításán van ‐ hiszen

Q^{*} Q^{* *}

P^{*}

-nál kilép a négyszögből. A további

P_{i}

pontok

(i = 2,3,4)

eseteinek előkészítéséül fölírjuk (1) módosulását ebben a változatban:

\begin{matrix} A B P^{*} & = A B Q^{* *} = A C B + A C Q^{* *} = A C B + A C F = A B C F = \\ = B F A + B F C = (B D A + B D C) / 2 = A B C D / 2 = t . \end{matrix}

A hasonló meggondolások nem a

P_{i}

helyzete szerint alakulnak az első vagy az újabb mintára, hanem a

Q

-típusú segédpont helyzete szerint. Ahogyan a

P_{i}

pontok közül csak kettő lehet magán a négyszög kerületén, ugyanúgy a segédpontok közül is, akár az

E

-n átmenő,

B D

-vel párhuzamos egyenes révén szerkesztjük őket, akár az

F

-en átmenő,

A C

-vel párhuzamos révén.