Kezdőlap


Feladat:	F.2178	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1979/április, 160 - 161. oldal		PDF \| MathML
Témakör(ök):	Trigonometriai azonosságok, Fermat-féle pont, Feladat, Középponti és kerületi szögek
Hivatkozás(ok):	Feladatok: 1978/december: F.2178

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Nyilvánvalóan elég foglalkoznunk a körülírt kör $O$ középpontjától különböző $G$ pontok esetével. Válasszuk úgy a betűzést, hogy $B E$ legyen az $O$ -hoz legközelebbi átló ‐, illetve a legközelebbiek egyike, ha több ilyen van ‐ és $E G F$ az a $60^{\circ}$ -os szögtartomány, amelyiknek a belsejében van $O$ , esetleg éppen a $G E$ szakaszon. Jelöljük még az $A D$ , $B E$ , $C F$ szakasz felezőpontját ( $O$ vetületét e húrokon) rendre $T_{1}$ , $T_{2}$ , $T_{3}$ -mal. Ekkor $O T_{2} \leq {O T}_{3}$ , $O G T_{2} ∢ \leq {O G T}_{3} ∢$ és $O G D ∢ \leq 90^{\circ} \leq O G A ∢$ , továbbá $T_{1}$ , $T_{2}$ , $T_{3}$ rendre a $G D$ , $G E$ , $G F$ szakaszon van, esetleg $T_{1} = G$ vagy $T_{2} = O$ . A bizonyítandó állítás így írható át:

\begin{matrix} A T_{1} - G T_{1} + C T_{3} - G T_{3} + E T_{2} + G T_{2} = B T_{2} - G T_{2} + D T_{1} + G T_{1} + F T_{3} + G T_{3}, \end{matrix}

és ez ekvivalens a következővel:

\begin{matrix} G T_{2} = G T_{1} + G T_{3}, \end{matrix}

(1)

ezt bizonyítjuk.

T

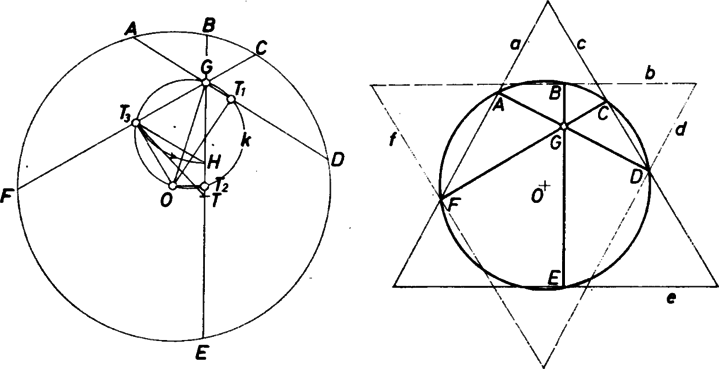-pontjaink nyilvánvalóan az

O G

szakasz mint átmérő fölötti

k

Thalész-körön vannak. A

T_{1} T_{2} T_{3}

háromszög szabályos, mert

T_{1} T_{2}

és

T_{2} T_{3}

oldalai

G

-ből

60 - 60^{\circ}

-os szögben láthatók. Mérjük föl

G

-ből

T_{2}

felé a

G H = G T_{3}

szakaszt és csatlakozóan a

H T = G T_{1}

szakaszt. Így

H G T_{3}

szabályos háromszög és

T_{3} H T ∢ = 120^{\circ} = T_{3} G T_{1} ∢

, ezek szerint pedig a

T H T_{3}

háromszög a

T_{1} G T_{3}

háromszög elfordított képe

60^{\circ}

-kal, ennélfogva

T

azonos

T_{2}

-vel. Így pedig

\begin{matrix} G T = G T_{2} = G H + H T_{2} = G T_{3} + G T_{1} . \end{matrix}

Ezt akartuk bizonyítani és ez ekvivalens a feladat állításával.

Megjegyzés. Goniometriai bizonyítás

(1)

-re: legyen

G O = 1

G O T_{1} ∢ = t

, ekkor

G O T_{3} ∢ = 60^{\circ} - t

és

G O T_{2} ∢ = 60^{\circ} + t

, és ezekkel

\begin{matrix} G T_{1} + G T_{3} = sin t + sin (60^{\circ} - t) = 2 sin 30^{\circ} cos \frac{60^{\circ} - 2 t}{2} = \\ = cos (30^{\circ} - t) = sin (60^{\circ} + t) = G T_{2} . \end{matrix}

Lényegében ez a számítás is szerepel a

3

fázisú váltakozóáram elméleti alapjai között.

II. megoldás. Állítsunk merőlegest mindegyik csúcsban az onnan induló átlóra és legyen az

A

-ban

A D

-re állított merőleges

a

, s í.t. Ekkor

a

c

és

e

, valamint

b

d

és

f

egy-egy háromszöget határoznak meg, és a merőleges szárú szögek alapján mindkét háromszög szabályos. Továbbá, mivel az átlók a kör húrjai, ezért az

a

és

d

...

párok egy-egy átmérőre és egyszersmind

O

-ra szimmetrikusan helyezkednek el, tehát a két háromszög

O

-ra középpontosan szimmetrikus helyzetű, emiatt egybevágó is.
Így a bizonyítandó egyenlőség két oldalán a

G

pontnak a két háromszög oldalaitól való távolságainak összege áll. Ismeretes, hogy egy szabályos háromszög belsejében (vagy kerületén) bárhol veszünk is fel egy pontot, annak távolságai a három oldaltól állandó összeget adnak, ti. a magasságot. És mivel a két szabályos háromszögünk egybevágó, függetlenül attól, hogy

G

hogyan helyezkedik el belsejükben, a két összeg egyenlő.

Megjegyzés. A feladat kiindulása folytán a

G

pont az

A C E

és

B D F

háromszögekre nézve (külön-külön) az ún. izogonális pont, amelyre nézve a

3

csúcstól mért távolságok összege minimális.